Rigged Hilbert space
A Hilbert space  containing a linear, everywhere-dense subset
containing a linear, everywhere-dense subset  , on which the structure of a topological vector space is defined, such that the imbedding is continuous. This imbedding generates a continuous imbedding of the dual space
, on which the structure of a topological vector space is defined, such that the imbedding is continuous. This imbedding generates a continuous imbedding of the dual space  and a chain of continuous imbeddings
and a chain of continuous imbeddings  (using the standard identification
(using the standard identification  ). The most interesting case is that in which
). The most interesting case is that in which  is a nuclear space. The following strengthening of the spectral theorem for self-adjoint operators acting on
is a nuclear space. The following strengthening of the spectral theorem for self-adjoint operators acting on  is true: Any self-adjoint operator
is true: Any self-adjoint operator  mapping
mapping  continuously (in the topology of
continuously (in the topology of 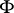 ) onto itself possesses a complete system of generalized eigenfunctions
) onto itself possesses a complete system of generalized eigenfunctions  (
( is a set of indices), i.e. elements
is a set of indices), i.e. elements  such that for any
such that for any 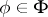 ,
,
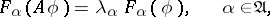 |
where the set of values of the function  ,
, 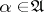 , is contained in the spectrum of
, is contained in the spectrum of 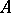 (cf. Spectrum of an operator) and has full measure with respect to the spectral measure
(cf. Spectrum of an operator) and has full measure with respect to the spectral measure 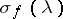 ,
, 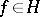 ,
,  , of any element
, of any element  . The completeness of the system means that
. The completeness of the system means that  for any
for any 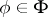 ,
, 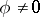 , for at least one
, for at least one 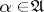 . Moreover, for any element
. Moreover, for any element  , its expansion with respect to the system of generalized eigenfunctions
, its expansion with respect to the system of generalized eigenfunctions 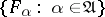 exists and generalizes the known expansion with respect to the basis of eigenvectors for an operator with a discrete spectrum.
exists and generalizes the known expansion with respect to the basis of eigenvectors for an operator with a discrete spectrum.
Example: The expansion into a Fourier integral
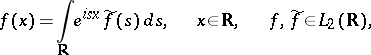 |
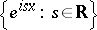 is a system of generalized eigenfunctions of the differentiation operator, acting on
is a system of generalized eigenfunctions of the differentiation operator, acting on 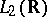 , arising under the natural rigging of this space by the Schwartz space
, arising under the natural rigging of this space by the Schwartz space  (cf. Generalized functions, space of). The same assertions are also correct for unitary operators acting on a rigged Hilbert space.
(cf. Generalized functions, space of). The same assertions are also correct for unitary operators acting on a rigged Hilbert space.
References
| [1] | I.M. Gel'fand, G.E. Shilov, "Some problems in the theory of differential equations" , Moscow (1958) (In Russian) |
| [2] | I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , 4 , Acad. Press (1964) (Translated from Russian) |
| [3] | Yu.M. [Yu.M. Berezanskii] Berezanskiy, "Expansion in eigenfunctions of selfadjoint operators" , Amer. Math. Soc. (1968) (Translated from Russian) |
Comments
A rigged Hilbert space  is also called a Gel'fand triple. Occasionally one also finds the phrases nested Hilbert space, or equipped Hilbert space.
is also called a Gel'fand triple. Occasionally one also finds the phrases nested Hilbert space, or equipped Hilbert space.
Rigged Hilbert space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Rigged_Hilbert_space&oldid=13083