Zariski tangent space
to an algebraic variety or scheme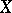 
at a point 
The vector space over the residue field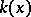 
of the point 
that is dual to the space 
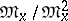, where 
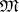is the maximal ideal of the local ring 
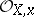of 
on 
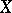. If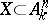 
is defined by a system of equations
 |
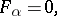where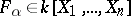 
, then the Zariski tangent space at a rational point 
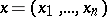is defined by the system of linear equations
 |
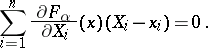A variety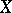 
is non-singular at a rational point 
if and only if the dimension of the Zariski tangent space to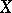 
at 
is equal to the dimension of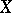 
. For a rational point 
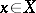, the Zariski tangent space is dual to the space 
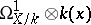— the stalk at 
of the cotangent sheaf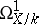 
. An irreducible variety 
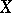over a perfect field 
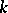is smooth if and only if the sheaf 
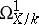is locally free. The vector bundle 
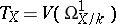associated with 
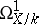is called the tangent bundle of 
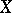over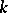 
; it is functorially related to 
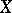. Its sheaf of sections is called the tangent sheaf to 
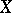. The Zariski tangent space was introduced by O. Zariski [1].
References
| [1] | O. Zariski, "The concept of a simple point of an abstract algebraic variety" Trans. Amer. Math. Soc. , 62 (1947) pp. 1–52 |
| [2] | P. Samuel, "Méthodes d'algèbre abstraite en géométrie algébrique" , Springer (1955) |
| [3] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
Comments
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2 |
Zariski tangent space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zariski_tangent_space&oldid=13053