Derived automorphism

in ergodic theory

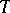A transformation defined by using an automorphism of a measure space and a measurable subset 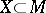of positive measure such that almost-all points of return to 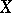under the action of iterates of 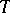. For every such point its image 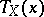is defined as that point of the trajectory 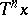at which this trajectory returns to for the first time after (according to the Poincaré recurrence theorem, cf. Poincaré return theorem, the condition for almost-all points of to return to at some time is automatically satisfied if 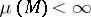). The transformation turns out to be an automorphism (more precisely, an automorphism modulo ) of the space 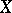with the measure induced on it (this measure is the measure 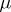considered only on subsets of ; if 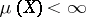then this measure is usually normalized).

Conversely, if 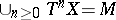(this condition is automatically satisfied if the automorphism 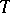is ergodic), then the original automorphism 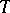can be recovered (up to conjugation by means of an isomorphism of measure spaces) from 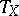and the time of first return

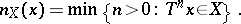Namely, 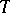is the special automorphism constructed from 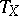and .

Comments

For automorphism of a measure space cf. Measure-preserving transformation.

In the literature also induced or derivative automorphism are used. See [a1] or [a2].

References

[a1]	S. Kakutani, "Induced measure preserving transformations" Proc. Japan. Acad. , 19 (1943) pp. 635–641
[a2]	K. Petersen, "Ergodic theory" , Cambridge Univ. Press (1983) pp. 39