Discriminant informant
A term in discriminant analysis denoting a variable used to establish a rule for assigning an object with measurements  , drawn from a mixture of
, drawn from a mixture of 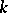 sets with distribution densities
sets with distribution densities 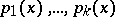 and a priori probabilities
and a priori probabilities 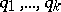 , to one of these sets. The
, to one of these sets. The 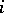 -th discriminant informant of the object with measurement
-th discriminant informant of the object with measurement  is defined as
is defined as
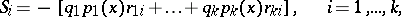 |
where 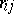 is the loss due to assigning an element from the distribution
is the loss due to assigning an element from the distribution 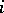 to the distribution
to the distribution 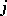 . The rule for assigning an object to the distribution with the largest discriminant informant has minimum mathematical expectation of the loss. In particular, if all
. The rule for assigning an object to the distribution with the largest discriminant informant has minimum mathematical expectation of the loss. In particular, if all 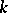 distributions are normal and have identical covariance matrices, all discriminant informants are linear. Then, if
distributions are normal and have identical covariance matrices, all discriminant informants are linear. Then, if 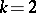 , the difference
, the difference 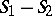 is Fisher's linear discriminant function.
is Fisher's linear discriminant function.
References
| [1] | C.R. Rao, "Linear statistical inference and its applications" , Wiley (1965) |
Discriminant informant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Discriminant_informant&oldid=13021