Double-sweep method

A method for transferring a one-point boundary condition by means of a differential or difference equation corresponding to the given equation. It is used for solving boundary value problems when the shooting method is ineffective.

Suppose one is given, on an interval , the linear ordinary differential equation

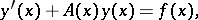(1)

where the square matrix 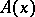has order , 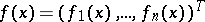is a vector of known continuous functions, and where the differentiable vector function 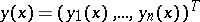has to be determined. Boundary conditions of the form

(2)

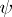are added to (1). Here, and are known matrices of dimension 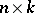and 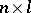and rank 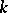and 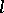, respectively,

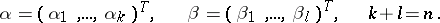By using the differential equations

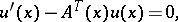with initial conditions 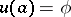, , where the unknown differentiable matrix function 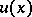has dimension 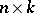and 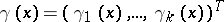, one can determine 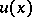and 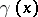on the whole interval 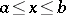(direct double-sweep). Using the equation

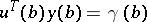and the second equation of (2) one can determine 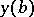, if the square matrix 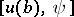has rank . The unknown solution of the boundary value problem (1)–(2) can now be computed as the solution of the Cauchy problem for (1) in the direction from the point 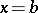to the point (inverse double-sweep). The method indicated is also applicable to multi-point problems, when constraints of the form (2) are given not only at the end points, but also at some interior points of 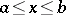. Versions of the double-sweep method for transferring linear boundary conditions different from (2) have been developed (cf. [1]).

The merit of the double-sweep method is obvious in the following boundary value problem

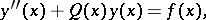(3)

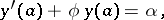(4)

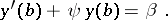(5)

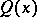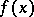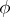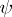Here, is a square matrix of order , is a vector of dimension of known continuous functions, the twice-differentiable vector function is to be determined, and are known square matrices of order , , 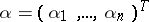and 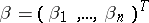. By using the differential equations

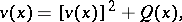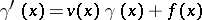with initial conditions 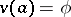, , 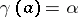one can determine 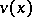and 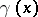on the whole interval 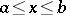(direct double-sweep). Here, 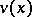is a differentiable square matrix of order and .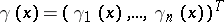

Using the equations

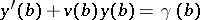and (5) one can determine

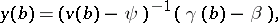(6)

if the matrix 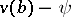has rank . The required solution of the boundary value problem (3)–(5) is the solution of the Cauchy problem for the equation

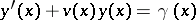with initial condition (6) (inverse double-sweep). Thus, the double-sweep method for (3)–(5) is a method lowering the order of the differential equation (3).

In the case of a finite sequence of linear algebraic equations

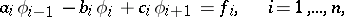(7)

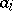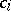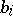where the coefficients , and are known square matrices of order and 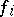, 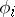are the known and required column-vectors of dimension , , 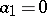, the double-sweep algorithm can be defined as follows:

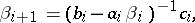(8)

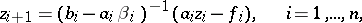(9)

under the conditions 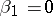, (direct) and

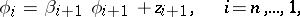(10)

under the condition 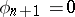(inverse). Here 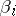is a square matrix of order and 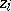, 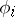are column-vectors of dimension . The method indicated is called right double-sweep. Analogous to (8)–(10) one obtains the formulas for left double-sweep. By combining left and right double-sweeps, one obtains the method of meeting double-sweep. In solving (7) with variable coefficients one applies the preparatory double-sweep method. In order to find periodic solutions of an infinite sequence of equations of the form (7) with periodic coefficients one uses cyclic double-sweep (cf. [4]).

See also Orthogonal double-sweep method.

References

[1]	N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian)
[2]	V.I. Krylov, V.V. Bobkov, P.I. Monastyrnyi, "Numerical methods" , 2 , Moscow (1977) (In Russian)
[3]	G.I. Marchuk, "Methods of numerical mathematics" , Springer (1982) (Translated from Russian)
[4]	A.A. Samarskii, E.S. Nikolaev, "Numerical methods for grid equations" , 1–2 , Birkhäuser (1989) (Translated from Russian)

References

[a1]	S.M. Roberts, J.S. Shipman, "Two point boundary value problems: shooting methods" , Amer. Elsevier (1972)
[a2]	U.M. Ascher, R.M.M. Mattheij, R.D. Russell, "Numerical solution for boundary value problems for ordinary differential equations" , Prentice-Hall (1988)