Fermat's little theorem
From Encyclopedia of Mathematics
For a number 
not divisible by a prime number 
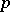, the congruence 
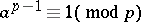holds. This theorem was established by P. Fermat (1640). It proves that the order of every element of the multiplicative group of residue classes modulo 
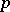divides the order of the group. Fermat's little theorem was generalized by L. Euler to the case modulo an arbitrary 
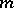. Namely, he proved that for every number 
relatively prime to the given number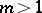 
there is the congruence
 |
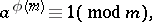where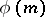 
is the Euler function. Another generalization of Fermat's little theorem is the equation 
, which is valid for all elements of the finite field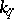 
consisting of 
elements.
References
| [1] | I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian) |
Comments
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) |
How to Cite This Entry:
Fermat's little theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fermat%27s_little_theorem&oldid=12998
Fermat's little theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fermat%27s_little_theorem&oldid=12998
This article was adapted from an original article by S.A. Stepanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article