First integral

of an ordinary differential equation

A non-constant continuously-differentiable function whose derivative vanishes identically on the solutions of that equation. For a scalar equation

(*)

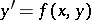a first integral is a function which occurs in the general solution , where is an arbitrary constant. Therefore, satisfies the linear equation

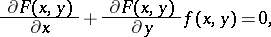containing first-order partial derivatives. A first integral need not exist throughout the domain of definition of (*), but it always exists in a small region around a point at which is continuously differentiable. A first integral is not uniquely defined. For example, for the equation , a first integral is not only but also, e.g., .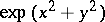

Knowledge of a first integral for a normal system

enables one to reduce the order of this system by one, while the search for functionally-independent first integrals is equivalent to the search for the general solution in implicit form. If 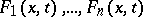are functionally-independent first integrals, then any other first integral 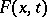can be put in the form

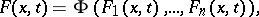where 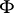is some differentiable function.

References

[1]	L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) (Translated from Russian)