Homogeneous convex cone

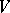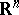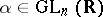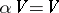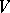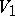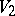An open strictly-convex cone in the vector space that is homogeneous with respect to the group of linear transformations for which (the so-called automorphisms of the cone ). Two homogeneous convex cones and are called isomorphic if there exists an isomorphism of the ambient vector spaces taking 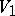onto .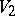

Examples.

1) The spherical cone

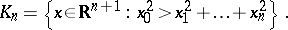The automorphism group of is the direct product of a subgroup of index 2 of the Lorentz group 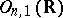(isomorphic to the group of motions of the -dimensional Lobachevskii space) and the group 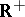of homotheties with positive coefficients.

2) The cone 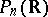of positive-definite real symmetric matrices of order . The automorphism group of this cone consists of the transformations

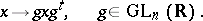3) The cone 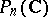of positive-definite complex Hermitian matrices of order .

4) The cone 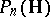of positive-definite quaternion Hermitian matrices of order .

The convex cone 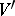dual to the homogeneous convex cone (i.e. the cone in the dual space consisting of all linear forms that are positive on ) is also homogeneous. A homogeneous convex cone 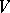is called self-dual if there exists a Euclidean metric on the ambient vector space 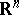such that 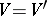under the identification of 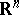with its dual by means of this metric. All the examples of homogeneous convex cones given above are self-dual.

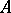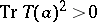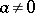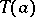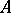The classification of self-dual homogeneous convex cones is based on their relation with compact Jordan algebras (cf. Jordan algebra) (see [1]), [2]). A real Jordan algebra is called compact if for all , , where is the operator of multiplication by in the algebra . Complexification establishes a one-to-one correspondence between the classes of isomorphic compact Jordan algebras and the classes of isomorphic semi-simple complex Jordan algebras. The set of squares of invertible elements of a compact Jordan algebra is a self-dual homogeneous convex cone, and all self-dual homogeneous convex cones can be obtained in this way. Hence it can be deduced that every self-dual homogeneous convex cone is isomorphic to a direct product of cones of the four types described above and a 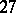-dimensional cone, related to the exceptional simple Jordan algebra.

An arbitrary homogeneous convex cone can be represented as a cone of positive-definite Hermitian matrices in a generalized matrix algebra . The simplest example of a non-self-dual homogeneous convex cone is the -dimensional cone of positive-definite symmetric real matrices 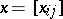of order 3 satisfying the condition 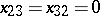. Starting with , there is a continuum of non-isomorphic homogeneous convex cones in .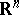

In every homogeneous convex cone a complete Riemannian metric can be defined in a canonical way, and it is invariant with respect to all its automorphisms. Self-dual homogeneous convex cones are characterized by the property that they are symmetric spaces (cf. Symmetric space) with respect to this metric. The stabilizer of any point in a homogeneous convex cone is a maximal compact subgroup of its automorphism group. The stabilizer of the identity of a compact Jordan algebra 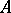in the automorphism group of the homogeneous convex cone associated with 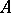coincides with the automorphism group of 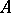. Every homogeneous convex cone admits a simply-transitive automorphism group, reducing to triangle form in some basis.

Homogeneous convex cones are of special interest in the theory of homogeneous bounded domains (cf. Homogeneous bounded domain) because these domains can be realized as Siegel domains (cf. Siegel domain), and for a Siegel domain of the first or second kind to be homogeneous it is necessary that the convex cone associated with it should be homogeneous. Homogeneous convex cones and their associated Siegel domains are natural carriers for certain analytic constructions, in particular generalizations of Eulerian integrals and hypergeometric functions [8]. With every homogeneous convex cone there is related a multi-parameter group of Riemann–Liouville integrals, including certain hyperbolic differential operators (for example, the wave operator is obtained in this way in the case of a spherical cone). The strengthened Huygens principle may hold [9] for these operators.

Investigation of discrete automorphism groups of self-dual homogeneous convex cones is important for the compactification and reduction of singularities of locally symmetric spaces [4]. Many results in classical reduction theory obtained for the group 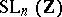acting on the cone can be generalized to arbitrary self-dual homogeneous convex cones (see [5], [6]).

References

[1]	M. Koecher, "Die Geodätischen von Positivitätsbereichen" Math. Ann. , 135 : 3 (1958) pp. 192–202
[2]	E.B. Vinberg, "Homogeneous cones" Soviet Math. Dokl. , 1 (1960) pp. 787–790 Dokl. Akad. Nauk SSSR , 133 : 1 (1960) pp. 9–12
[3a]	E.B. Vinberg, "The theory of convex homogeneous cones" Trans. Amer. Math. Soc. , 12 (1963) pp. 340–403 Trudy Moskov. Mat. Obshch. , 12 (1963) pp. 303–358
[3b]	E.B. Vinberg, "The structure of the structure group of automorphisms of a homogeneous convex cone" Trans. Amer. Math. Soc. , 13 (1965) pp. 63–93 Trudy Moskov. Mat. Obshch. , 13 (1965) pp. 56–83
[4]	A. Ash, et al., "Smooth compactification of locally symmetric varieties" , Math. Sci. Press (1975)
[5]	K.-H. Helwig, "Zur Koecherschen Reduktionstheorie in Positivitätsbereichen I-III" Mat. Z. , 91 (1966) pp. 152–168; 169–178; 355–362
[6]	A. Ash, "On entactic forms" Canad. J. Math. , 29 : 5 (1977) pp. 1040–1054
[7a]	O.S. Rothaus, "The construction of homogeneous convex cones" Ann. of Math. , 83 (1966) pp. 358–376
[7b]	O.S. Rothaus, "Correction to: The construction of homogeneous convex cones" Ann. of Math. , 87 (1968) pp. 399
[8]	S.G. Gindikin, "Analysis in homogeneous domains" Russian Math. Surveys , 19 : 4 (1964) pp. 1–89 Uspekhi Mat. Nauk , 19 : 4 (1964) pp. 3–92
[9]	B.R. Vainberg, S.G. Gindikin, "On the strong Huygens principle for a class of differential operators with constant coefficients" Trans. Amer. Math. Soc. , 16 (1967) pp. 163–196 Trudy Moskov. Mat. Obshch. , 16 (1967) pp. 151–180

References

[a1]	J. Faraut, A. Korányi, "Fonctions hypergéométriques associées aux cônes symétriques" C.R. Acad. Sci. Paris , 307 (1988) pp. 555–558