Kontorovich-Lebedev-transform(2)

The integral transform

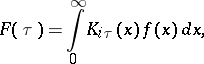where 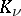is the Macdonald function.

If 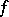is of bounded variation in a neighbourhood of a point and if

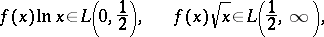then the following inversion formula holds:

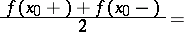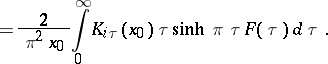Let 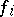, , 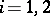be real-valued functions with

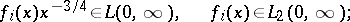and let

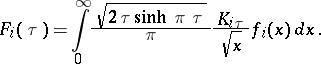Then

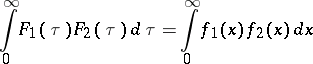(Parseval's identity).

The finite Kontorovich–Lebedev transform has the form

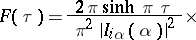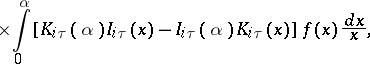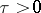, where 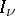is the modified Bessel function (see [3]).

The study of such transforms was initiated by M.I. Kontorovich and N.N. Lebedev (see [1], [2]).

References

[1]	M.I. Kontorovich, N.N. Lebedev, "A method for the solution of problems in diffraction theory and related topics" Zh. Eksper. i. Toer. Fiz. , 8 : 10–11 (1938) pp. 1192–1206 (In Russian)
[2]	N.N. Lebedev, Dokl. Akad. Nauk SSSR , 52 : 5 (1945) pp. 395–398
[3]	Ya.S. Uflyand, E. Yushkova, Dokl. Akad. Nauk SSSR , 164 : 1 (1965) pp. 70–72
[4]	V.A. Ditkin, A.P. Prudnikov, "Integral transforms and operational calculus" , Pergamon (1965) (Translated from Russian)

Comments

A transform table for the Kontorovich–Lebedev transform can be found in [a1]. A treatment in some detail of the transform is in [a2].

References

[a1]	A. Erdelyi, W. Magnus, F. Oberhettinger, "Tables of integral transforms" , 1–2 , McGraw-Hill (1954) pp. Chapt. XII
[a2]	I.N. Sneddon, "The use of integral transforms" , McGraw-Hill (1972) pp. Chapt. 6