Disjunctive elements
independent elements
Two elements 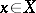 and
and 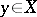 of a vector lattice
of a vector lattice  with the property
with the property
 |
Here
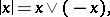 |
which is equivalent to
 |
The symbols 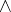 and
and  are, respectively, the disjunction and the conjunction. Two sets
are, respectively, the disjunction and the conjunction. Two sets  and
and  are called disjunctive if any pair of elements
are called disjunctive if any pair of elements  ,
,  is disjunctive. An element
is disjunctive. An element 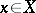 is said to be disjunctive with a set
is said to be disjunctive with a set 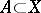 if the sets
if the sets 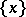 and
and  are disjunctive. A disjunctive pair of elements is denoted by
are disjunctive. A disjunctive pair of elements is denoted by  or
or 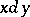 ; a disjunctive pair of sets is denoted by
; a disjunctive pair of sets is denoted by 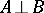 or
or  , respectively.
, respectively.
Example of disjunctive elements: The positive part 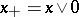 and the negative part
and the negative part 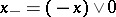 of an element
of an element  .
.
If the elements 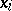 ,
, 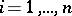 , are pairwise disjunctive, they are linearly independent; if
, are pairwise disjunctive, they are linearly independent; if 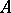 and
and 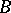 are disjunctive elements, the linear subspaces which they generate are also disjunctive; if
are disjunctive elements, the linear subspaces which they generate are also disjunctive; if  ,
,  , and
, and
 |
exists, then  . For disjunctive elements, several structural relations are simplified; e.g., if
. For disjunctive elements, several structural relations are simplified; e.g., if  , then
, then
 |
 |
for  , etc.
, etc.
The concept of disjunctive elements may also be introduced in more general partially ordered sets, such as Boolean algebras.
References
| [1] | L.V. Kantorovich, B.Z. Vulikh, A.G. Pinsker, "Functional analysis in semi-ordered spaces" , Moscow-Leningrad (1950) (In Russian) |
| [2] | B.Z. Vulikh, "Introduction to the theory of partially ordered spaces" , Wolters-Noordhoff (1967) (Translated from Russian) |
| [3] | N. Bourbaki, "Elements of mathematics. Integration" , Addison-Wesley (1975) pp. Chapt.6;7;8 (Translated from French) |
Comments
The phrase "disjunctive sets" also has a different meaning, cf. Disjunctive family of sets.
References
| [a1] | W.A.J. Luxemburg, A.C. Zaanen, "Riesz spaces" , I , North-Holland (1971) |
Disjunctive elements. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Disjunctive_elements&oldid=12766