Zone of normal attraction
A domain of the form 
for which
 |
as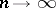 
, where 
, 
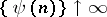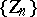is a sequence of random variables and 
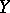is a random variable with a normal distribution. Zones of normal attraction have been studied for the case
 |
where 
is a sequence of independent, identically-distributed random variables with mathematical expectation 
and finite positive variance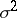 
.
References
| [1] | I.A. Ibragimov, Yu.V. Linnik, "Independent and stationary sequences of random variables" , Wolters-Noordhoff (1971) (Translated from Russian) |
Comments
A rather general formulation of the problems of large deviations is as follows, [a3]. Suppose that for a family of stochastic processes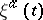 
a result of the law-of-large-numbers type holds (cf. Law of large numbers), 
as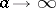 
. Problems on large deviations of the process 
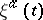from its most probable path 
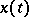for large values of 
are concerned with the limiting behaviour as 
of the infinitesimal probabilities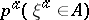 
for measurable sets 
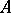that are at a positive distance from the non-random limiting function 
(in a suitable function space (space of paths)). Problems concerning the asymptotics as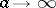 
of expectations of the form 
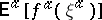also form part of large deviation theory if the main part of these expectations for large values of 
comes from the low probability values of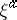 
.
References
| [a1] | V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian) |
| [a2] | R.J. Serfling, "Approximation theorems of mathematical statistics" , Wiley (1980) pp. 6, 96 |
| [a3] | A.D. [A.D. Ventsel'] Wentzell, "Limit theorems on large deviations for Markov stochastic processes" , Kluwer (1990) (Translated from Russian) |
| [a4] | L. Saulis, V.A. Statulevicius, "Limit theorems for large deviations" , Kluwer (1991) (Translated from Russian) |
Zone of normal attraction. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zone_of_normal_attraction&oldid=12758