Harmonizable dynamical system

A flow (continuous-time dynamical system) the trajectories of which become almost-periodic after a certain change of the time. An additional condition which is usually made is that each trajectory be everywhere-dense in the phase space (so that one may speak of a harmonizable minimal set).

Comments

In the above, an almost-periodic trajectory in a dynamical system 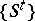on a metric space 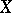is the trajectory of any point 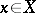which has the following property: For every 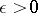the set of -almost periods,

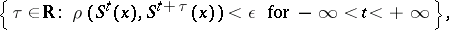is relatively-dense in 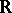, that is, there exists an 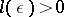such that every interval of length 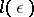contains an -almost period (compare this with the definition of almost-period of an almost-periodic function).