Jacobi brackets
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
Mayer brackets
The differential expression
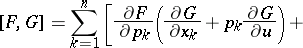 | (1) |
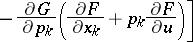 |
in the functions 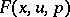 and
and  of
of 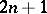 independent variables
independent variables 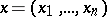 and
and 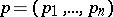 .
.
The main properties are:
1) 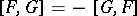 ;
;
2) 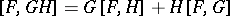 ;
;
3) if 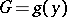 ,
, 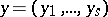 and
and 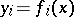 , then
, then 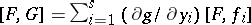 ;
;
4) 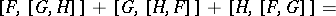
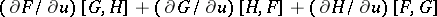 .
.
The last property is called the Jacobi identity (see [1], [2]).
The expression (1) is sometimes written in the form
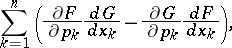 |
where the symbolic notation
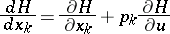 | (2) |
is used. If  and
and 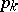 are regarded as functions of
are regarded as functions of 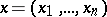 , and
, and 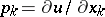 ,
, 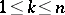 , then (2) gets the meaning of the total derivative with respect to
, then (2) gets the meaning of the total derivative with respect to 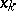 .
.
If 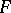 and
and 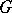 are independent of
are independent of  , then their Jacobi brackets (1) are Poisson brackets.
, then their Jacobi brackets (1) are Poisson brackets.
References
| [1] | C.G.J. Jacobi, "Nova methodus, aequationes differentiales partiales primi ordinis inter numerum variabilium quemcunque propositas integrandi" J. Reine Angew. Math. , 60 (1862) pp. 1–181 |
| [2] | A. Mayer, "Ueber die Weiler'sche Integrationsmethode der partiellen Differentialgleichungen erster Ordnung" Math. Ann. , 9 (1876) pp. 347–370 |
| [3] | N.M. Gyunter, "Integrating first-order partial differential equations" , Leningrad-Moscow (1934) (In Russian) |
| [4] | W.W. [V.V. Stepanov] Stepanow, "Lehrbuch der Differentialgleichungen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
Comments
The Poisson brackets are an essential tool in classical mechanics, cf. e.g. [a1].
References
| [a1] | V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) |
How to Cite This Entry:
Jacobi brackets. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jacobi_brackets&oldid=12643
Jacobi brackets. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jacobi_brackets&oldid=12643
This article was adapted from an original article by A.P. Soldatov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article