Complexification of a Lie algebra

over

The complex Lie algebra that is the tensor product of the algebra with the complex field over the field of real numbers :

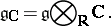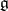Thus, the complexification of the Lie algebra is obtained from by extending the field of scalars from 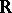to 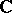. As elements of the algebra one can consider pairs 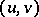, 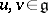; the operations in are then defined by the formulas:

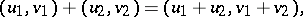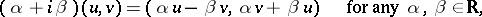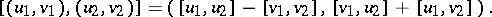The algebra is also called the complex hull of the Lie algebra .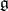

Certain important properties of an algebra are preserved under complexification: 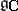is nilpotent, solvable or semi-simple if and only if has this property. However, simplicity of does not, in general, imply that of .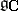

The notion of the complexification of a Lie algebra is closely related to that of a real form of a complex Lie algebra (cf. Form of an (algebraic) structure). A real Lie subalgebra 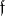of a complex Lie algebra is called a real form of 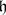if each element is uniquely representable in the form 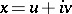, where . The complexification of 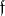is naturally isomorphic to 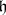. Not every complex Lie algebra has a real form. On the other hand, a given complex Lie algebra may, in general, have several non-isomorphic real forms. Thus, the Lie algebra of all real matrices of order and the Lie algebra of all anti-Hermitian matrices of order are non-isomorphic real forms of the Lie algebra of all complex matrices of order (which also has other real forms).

References

[1]	M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian)
[2]	D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian)
[3]	F. Gantmakher, "On the classification of real simple Lie groups" Mat. Sb. , 5 : 2 (1939) pp. 217–250