Regular representation
The (left) regular representation of an algebra 
is the linear representation 
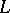of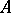 
on the vector space 
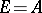defined by the formula 
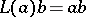for all 
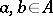. Similarly, the formula 
, 
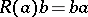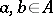, defines an (anti-) representation of 
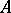on the space 
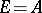, called the (right) regular representation of 
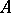. If 
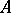is a topological algebra (with continuous multiplication in all the variables), then 
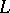and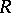 
are continuous representations. If 
is an algebra with a unit element or a semi-simple algebra, then its regular representations are faithful (cf. Faithful representation).
A (right) regular representation of a group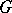 
is a linear representation 
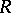of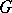 
on a space 
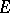of complex-valued functions on 
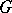, defined by the formula
 |
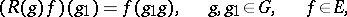provided that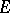 
separates the points of 
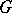and has the property that the function 
, 
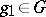, belongs to 
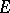for all 
, 
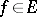. Similarly, the formula
 |
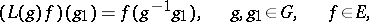defines a (left) regular representation of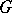 
on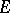 
, where the function 
, 
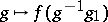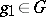, is assumed to belong to 
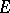for all 
, 
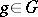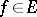. If 
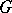is a topological group, then 
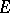is often the space of continuous functions on 
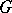. If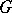 
is locally compact, then the (right) regular representation of 
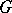is the (right) regular representation of 
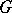on the space 
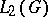constructed by means of the right-invariant Haar measure on 
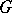; the regular representation of a locally compact group is a continuous unitary representation, and the left and right regular representations are unitarily equivalent.
Comments
References
| [a1] | C.W. Curtis, I. Reiner, "Methods of representation theory" , 1–2 , Wiley (Interscience) (1981–1987) |
Regular representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_representation&oldid=12625