Bordering of a space
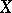 in a compactification
in a compactification 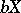
A finite family 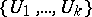 of sets open in
of sets open in 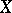 such that the set
such that the set 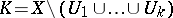 is compact, and
is compact, and 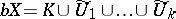 , where
, where 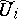 is the largest open set in
is the largest open set in 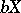 the intersection of which with
the intersection of which with 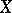 is the set
is the set 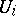 (
(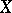 is assumed to be completely regular). The concept of a bordering of a space
is assumed to be completely regular). The concept of a bordering of a space 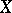 in
in 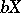 coincides with the concept of an almost-extendable bordering of a proximity space
coincides with the concept of an almost-extendable bordering of a proximity space 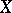 (the proximity on
(the proximity on 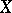 is induced by the extension
is induced by the extension 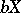 ), formulated in terms of the proximity: apart from
), formulated in terms of the proximity: apart from 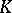 being compact, it is necessary that for any neighbourhood
being compact, it is necessary that for any neighbourhood 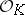 , the family
, the family 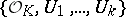 is a uniform covering of the space
is a uniform covering of the space 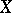 . A bordering of a space
. A bordering of a space 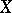 in its Stone–Čech compactification is simply called a bordering of
in its Stone–Čech compactification is simply called a bordering of 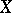 . In the language of borderings, a series of theorems has been formulated on the dimensions of the remainder of compactifications of topological and proximity spaces.
. In the language of borderings, a series of theorems has been formulated on the dimensions of the remainder of compactifications of topological and proximity spaces.
References
| [1] | Yu.M. Smirnov, "On the dimensions of remainders of compactifications of proximity and topological spaces" Mat. Sb. , 71 : 4 (1966) pp. 554–482 (In Russian) |
Comments
A concept related to the bordering of a space is that of a border cover: A collection 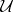 of open sets such that
of open sets such that 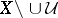 is compact. Border covers work in a sense opposite to borderings. In the case of borderings a compactification is given; from certain systems of border covers one can construct compactifications whose remainders can have special properties.
is compact. Border covers work in a sense opposite to borderings. In the case of borderings a compactification is given; from certain systems of border covers one can construct compactifications whose remainders can have special properties.
Bordering of a space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bordering_of_a_space&oldid=12603