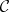
A contravariant functor 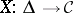 (or, equivalently, a covariant functor
(or, equivalently, a covariant functor 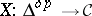 ) from the category
) from the category 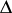 , whose objects are ordered sets
, whose objects are ordered sets 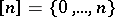 ,
, 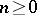 , and whose morphisms are non-decreasing mappings
, and whose morphisms are non-decreasing mappings 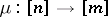 , into the category
, into the category 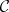 . A covariant functor
. A covariant functor 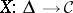 (or, equivalently, a contravariant functor
(or, equivalently, a contravariant functor  ) is called a co-simplicial object in
) is called a co-simplicial object in 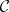 .
.
The morphisms
of  given by
given by
generate all the morphisms of 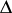 , so that a simplicial object
, so that a simplicial object 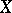 is determined by the objects
is determined by the objects 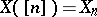 ,
, 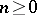 (called the
(called the  -fibres or
-fibres or  -components of the simplicial object
-components of the simplicial object 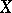 ), and the morphisms
), and the morphisms
(called boundary operators and degeneracy operators, respectively). In case 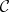 is a category of structured sets, the elements of
is a category of structured sets, the elements of 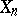 are usually called the
are usually called the  -dimensional simplices of
-dimensional simplices of 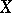 . The mappings
. The mappings 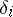 and
and 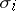 satisfy the relations
satisfy the relations
 | (*) |
and any relation between these mappings is a consequence of the relations (*). This means that a simplicial object 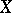 can be identified with a system
can be identified with a system 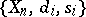 of objects
of objects 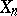 ,
, 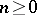 , of
, of 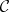 and morphisms
and morphisms 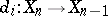 and
and 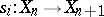 ,
, 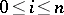 , satisfying the relations
, satisfying the relations
Similarly, a co-simplicial object 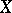 can be identified with a system
can be identified with a system 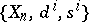 of objects
of objects 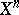 ,
, 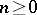 (
( -co-fibres) and morphisms
-co-fibres) and morphisms 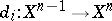 ,
, 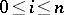 (co-boundary operators), and
(co-boundary operators), and 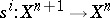 ,
, 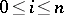 (co-degeneracy operators), satisfying the relations (*) (with
(co-degeneracy operators), satisfying the relations (*) (with 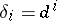 ,
, 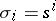 ).
).
A simplicial mapping  between simplicial objects (in the same category
between simplicial objects (in the same category 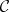 ) is a transformation (morphism) of functors from
) is a transformation (morphism) of functors from 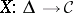 into
into 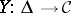 , that is, a family of morphisms
, that is, a family of morphisms 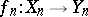 ,
, 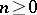 , of
, of  such that
such that
The simplicial objects of 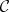 and their simplicial mappings form a category, denoted by
and their simplicial mappings form a category, denoted by 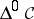 .
.
A simplicial homotopy 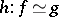 between two simplicial mappings
between two simplicial mappings 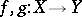 between simplicial objects in a category
between simplicial objects in a category 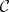 is a family of morphisms
is a family of morphisms 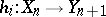 ,
, 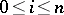 , of
, of 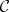 such that
such that
On the basis of this definition one can reproduce in essence the whole of ordinary homotopy theory in the category 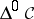 , for any category
, for any category 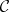 . In the case of the category of sets or topological spaces, the geometric realization functor (see Simplicial set) carries this "simplicial" theory into the usual one.
. In the case of the category of sets or topological spaces, the geometric realization functor (see Simplicial set) carries this "simplicial" theory into the usual one.
Examples of simplicial objects are a simplicial set, a simplicial topological space, a simplicial algebraic variety, a simplicial group, a simplicial Abelian group, a simplicial Lie algebra, a simplicial smooth manifold, etc.
Every simplicial Abelian group can be made into a chain complex with boundary operator 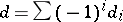 .
.
References
| [1] | P. Gabriel, M. Zisman, "Calculus of fractions and homotopy theory" , Springer (1967) |
| [2] | J.P. May, "Simplicial objects in algebraic topology" , v. Nostrand (1967) |
| [3] | K. Lamotke, "Semisimpliziale algebraische Topologie" , Springer (1968) |
How to Cite This Entry:
Simplicial object in a category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Simplicial_object_in_a_category&oldid=12531
This article was adapted from an original article by S.N. MalyginM.M. Postnikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article
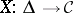 (or, equivalently, a covariant functor
(or, equivalently, a covariant functor 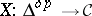 ) from the category
) from the category 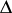 , whose objects are ordered sets
, whose objects are ordered sets 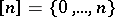 ,
, 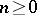 , and whose morphisms are non-decreasing mappings
, and whose morphisms are non-decreasing mappings 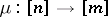 , into the category
, into the category 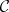 . A covariant functor
. A covariant functor 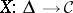 (or, equivalently, a contravariant functor
(or, equivalently, a contravariant functor  ) is called a co-simplicial object in
) is called a co-simplicial object in 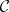 .
.
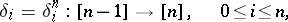
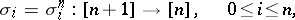
 given by
given by
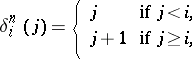
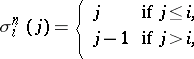
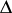 , so that a simplicial object
, so that a simplicial object 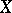 is determined by the objects
is determined by the objects 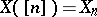 ,
, 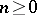 (called the
(called the  -fibres or
-fibres or  -components of the simplicial object
-components of the simplicial object 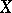 ), and the morphisms
), and the morphisms

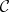 is a category of structured sets, the elements of
is a category of structured sets, the elements of 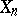 are usually called the
are usually called the  -dimensional simplices of
-dimensional simplices of 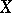 . The mappings
. The mappings 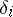 and
and 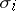 satisfy the relations
satisfy the relations

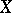 can be identified with a system
can be identified with a system 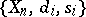 of objects
of objects 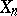 ,
, 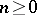 , of
, of 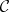 and morphisms
and morphisms 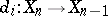 and
and 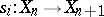 ,
, 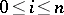 , satisfying the relations
, satisfying the relations
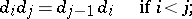
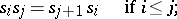

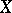 can be identified with a system
can be identified with a system 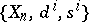 of objects
of objects 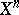 ,
, 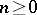 (
( -co-fibres) and morphisms
-co-fibres) and morphisms 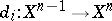 ,
, 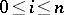 (co-boundary operators), and
(co-boundary operators), and 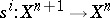 ,
, 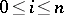 (co-degeneracy operators), satisfying the relations (*) (with
(co-degeneracy operators), satisfying the relations (*) (with 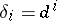 ,
, 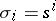 ).
).
 between simplicial objects (in the same category
between simplicial objects (in the same category 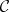 ) is a transformation (morphism) of functors from
) is a transformation (morphism) of functors from 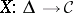 into
into 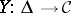 , that is, a family of morphisms
, that is, a family of morphisms 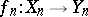 ,
, 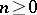 , of
, of  such that
such that
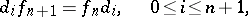
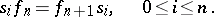
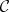 and their simplicial mappings form a category, denoted by
and their simplicial mappings form a category, denoted by 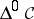 .
.
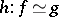 between two simplicial mappings
between two simplicial mappings 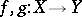 between simplicial objects in a category
between simplicial objects in a category 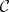 is a family of morphisms
is a family of morphisms 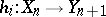 ,
, 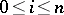 , of
, of 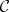 such that
such that
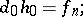
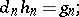
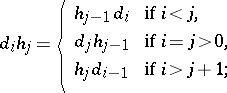

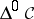 , for any category
, for any category 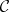 . In the case of the category of sets or topological spaces, the geometric realization functor (see Simplicial set) carries this "simplicial" theory into the usual one.
. In the case of the category of sets or topological spaces, the geometric realization functor (see Simplicial set) carries this "simplicial" theory into the usual one.
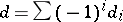 .
.