Separable completion of a ring

The completion of the topological ring , where is a topological ring and is the closure in of the zero ideal . The separable completion of a ring is also a topological ring and is usually denoted by . Every continuous homomorphism from into a complete separable ring can be uniquely extended to a continuous homomorphism .

In the most important case where the topology of the ring 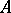is linear and is defined by a fundamental system of ideals , the separable completion 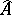is canonically identified with the projective limit 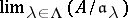of the discrete rings 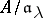. The separable completion of a module is achieved in the same way.

References

[a1]	N. Bourbaki, "Algèbre commutative" , Eléments de mathématiques , Hermann (1961) pp. Chapt. 3. Graduations, filtrations, et topologies