Transcendental branch point
From Encyclopedia of Mathematics
of an analytic function 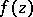
A branch point that is not an algebraic branch point. In other words, it is either a branch point  of finite order
of finite order  at which, however, there does not exist a finite or infinite limit
at which, however, there does not exist a finite or infinite limit
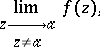 |
or a logarithmic branch point of infinite order. For example, the first possibility is realized at the transcendental branch point 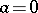 for the function
for the function 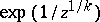 , the second for the function
, the second for the function  .
.
In the first case the function 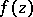 can be expanded in a neighbourhood of
can be expanded in a neighbourhood of  in the form of a Puiseux series
in the form of a Puiseux series
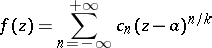 |
with an infinite number of non-zero coefficients 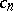 with negative indices.
with negative indices.
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 2 , Chelsea (1977) (Translated from Russian) |
How to Cite This Entry:
Transcendental branch point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transcendental_branch_point&oldid=12387
Transcendental branch point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transcendental_branch_point&oldid=12387
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article