Mutually-prime numbers
From Encyclopedia of Mathematics
coprimes, relatively-prime numbers
Integers without common (prime) divisors. The greatest common divisor of two coprimes  and
and 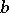 is 1, which is usually written as
is 1, which is usually written as 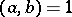 . If
. If  and
and 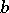 are coprime, there exist numbers
are coprime, there exist numbers  and
and  ,
, 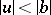 ,
, 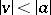 , such that
, such that 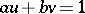 .
.
The concept of being coprime may also be applied to polynomials and, more generally, to elements of a Euclidean ring.
Comments
References
| [a1] | I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian) |
How to Cite This Entry:
Mutually-prime numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mutually-prime_numbers&oldid=12368
Mutually-prime numbers. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mutually-prime_numbers&oldid=12368