Polyhedral complex
A finite set of closed convex polytopes in a certain  which together with each polytope contains all its faces and is such that the intersection between the polytopes is either empty or is a face of each of them. An example of a polyhedral complex is the set of all vertices, edges and two-dimensional faces of the standard three-dimensional cube. One considers also complexes consisting of an infinite but locally finite family of polytopes. The concept of a polyhedral complex generalizes the concept of a geometric simplicial complex. The underlying space
which together with each polytope contains all its faces and is such that the intersection between the polytopes is either empty or is a face of each of them. An example of a polyhedral complex is the set of all vertices, edges and two-dimensional faces of the standard three-dimensional cube. One considers also complexes consisting of an infinite but locally finite family of polytopes. The concept of a polyhedral complex generalizes the concept of a geometric simplicial complex. The underlying space 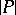 of a polyhedral complex
of a polyhedral complex 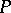 is the union of all polytopes entering into it and is itself an (abstract) polyhedron (cf. Polyhedron, abstract). The number of polytopes in
is the union of all polytopes entering into it and is itself an (abstract) polyhedron (cf. Polyhedron, abstract). The number of polytopes in 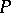 as a rule is less than the number of simplices in a triangulation. A polyhedral complex
as a rule is less than the number of simplices in a triangulation. A polyhedral complex 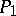 is called a subdivision of a complex
is called a subdivision of a complex  if their underlying spaces coincide and if each polytope from
if their underlying spaces coincide and if each polytope from  lies in a certain polytope from
lies in a certain polytope from 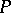 . A star-like subdivision of a complex
. A star-like subdivision of a complex  with centre at a point
with centre at a point  is obtained by means of a decomposition of the closed polytopes containing
is obtained by means of a decomposition of the closed polytopes containing  into cones with vertices at
into cones with vertices at  over those faces that do not contain
over those faces that do not contain  . Any polyhedral complex
. Any polyhedral complex  has a subdivision
has a subdivision 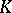 that is a geometric simplicial complex. Such a subdivision can be obtained without adding new vertices. It is sufficient, for example, to carry out in sequence the star-like subdivisions of
that is a geometric simplicial complex. Such a subdivision can be obtained without adding new vertices. It is sufficient, for example, to carry out in sequence the star-like subdivisions of  with centres at all the vertices of
with centres at all the vertices of 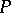 .
.
References
| [1] | P.S. Aleksandrov, "Combinatorial topology" , Graylock , Rochester (1956) (Translated from Russian) |
Comments
For extra references see also Polyhedral chain and Simplicial complex.
Polyhedral complex. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Polyhedral_complex&oldid=12367