Sierpiński game

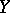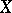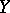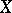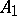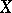Let be a topological space and an uncountable subset of . Two players alternatively select subsets of . Player I selects some uncountable subset of . Player II answers by picking up an uncountable subset 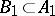. Then again player I selects some uncountable set 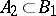and player II responds by selecting some uncountable subset 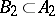. Playing this way the two players generate a decreasing sequence 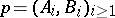of uncountable sets, which is called a play. By definition, player II wins this play if the intersection 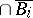of the closures of 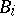(in 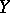) is contained in 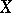. Otherwise the play is won by player I. A given "rule" of selecting the moves of player II is called a winning strategy for player II if every play generated by this rule is won by this player.

If 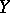is a Polish space (a completely metrizable and separable space, cf. also Vague topology; Descriptive set theory; Complete metric space; Separable space), then the existence of a winning strategy for player II implies that 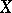contains the Cantor discontinuum (and therefore contains continuum many points). On the other hand, if 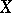is a Suslin subset of 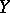(cf. also Descriptive set theory), then player II has a winning strategy ([a3]). Thus, every uncountable Suslin subset of a Polish space contains the Cantor discontinuum. For Borel subsets of the unit segment this was proved by P.S. Aleksandrov ([a1] and Borel set) and F. Hausdorff ([a2]) when they were verifying the truth of the continuum hypothesis for such subsets of the unit segment. W. Sierpiński ([a5]) gave another proof of the same result. It was this proof of Sierpiński that made R. Telgársky ([a6]) introduce the above game and name it after Sierpiński. Further information concerning the game of Sierpiński can be found in [a3], [a4] and [a7].

References

[a1]	P.S. Alexandrov, "Sur la puissance des ensembles mesurables B" C.R. Acad. Sci. Paris , 162 (1916) pp. 323–325
[a2]	F. Hausdorff, "Die Mächtigkeit der Borelschen Mengen" Math. Ann. , 77 (1916) pp. 430–437
[a3]	G. Kubicki, "On a game of Sierpiński" Colloq. Math. , 54 (1987) pp. 179–192
[a4]	G. Kubicki, "On a modified game of Sierpiński" Colloq. Math. , 53 (1987) pp. 81–91
[a5]	W. Sierpiński, "Sur le puissance des ensembles mesurables (B)" Fundam. Math. , 5 (1924) pp. 166–171
[a6]	R. Telgárski, "On some topological games" , Proc. Fourth Prague Topological Symp. 1976, Part B: Contributed papers , Soc. Czech. Math. and Physicists (1977) pp. 461–472
[a7]	R. Telgárski, "Topological games: On the 50th anniversary of the Banach–Mazur game" Rocky Mount. J. Math. , 17 (1987) pp. 227–276