Compact set, countably
A set 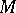 in a topological space
in a topological space 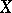 that as a subspace of this space is countably compact (cf. Compact space, countably). Countable compactness means that every sequence has an accumulation point, i.e. a point every neighbourhood of which contains infinitely many terms of the sequence.
that as a subspace of this space is countably compact (cf. Compact space, countably). Countable compactness means that every sequence has an accumulation point, i.e. a point every neighbourhood of which contains infinitely many terms of the sequence.
A topological space 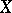 is called sequentially compact if every sequence has a converging subsequence, i.e. if every sequence has a subsequence converging to some point of
is called sequentially compact if every sequence has a converging subsequence, i.e. if every sequence has a subsequence converging to some point of 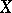 .
.
A set 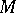 in a topological space
in a topological space 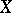 is called relatively (sequentially, countably) compact if its closure has the corresponding property.
is called relatively (sequentially, countably) compact if its closure has the corresponding property.
A set 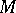 in a topological space
in a topological space 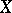 such that every infinite sequence
such that every infinite sequence 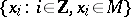 has a subsequence converging to some point
has a subsequence converging to some point 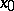 of
of 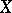 (respectively, has an accumulation point) could be called conditionally sequentially compact (respectively, conditionally countably compact).
(respectively, has an accumulation point) could be called conditionally sequentially compact (respectively, conditionally countably compact).
Comments
In metric spaces and Banach spaces with the weak topology the notions of compactness, sequential compactness and countable compactness coincide.
References
| [a1] | A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian) |
Compact set, countably. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Compact_set,_countably&oldid=12336