Hadamard variational formula

The formula

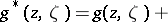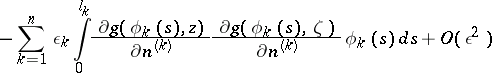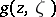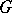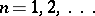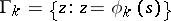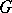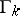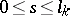for the Green function of an -connected domain () in the complex -plane. Hadamard's variational formula is applicable if: 1) the boundary components of the domain are twice-differentiable closed Jordan curves, where is the arc length on , ; 2) the numbers 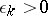are so small that the ends of the segments of the interior normals 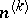to 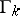of length 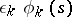lying in 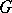form continuously-differentiable curves, bounding an -connected domain 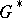, 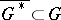; and 3) 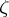is a fixed point in 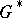. Hadamard's variational formula represents the Green function 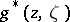of the domain 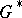by 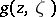with a uniform estimate 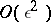, , 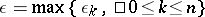of the remainder term in the direct product of the domain 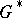and an arbitrary compact set in 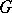. Hadamard's variational formula can also be used for the Green function of a finite Riemann surface with boundary.

The formula was proposed by J. Hadamard [1].

References

[1]	J. Hadamard, "Memoire sur le problème d'analyse relatif a l'équilibre des plagues élastiques eucastrées" Mém. prés. par divers savants à l'Acad. Sci. , 33 (1907) (Also: Oeuvres, Vol. II, C.N.R.S. (1968), pp. 515–631)
[2]	M. Schiffer, D.C. Spencer, "Functionals of finite Riemann surfaces" , Princeton Univ. Press (1954)

Comments

For a proof of Hadamard's variational formula under minimal hypotheses, plus further references, see [a1].

References

[a1]	S.E. Warschawski, "On Hadamard's variation formula for Green's function" J. Math. Mech. , 9 (1960) pp. 497–511