Compactness principle
in the theory of functions of a complex variable
The condition of compactness of families of analytic functions. An infinite family  of holomorphic functions in a domain
of holomorphic functions in a domain 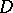 of the complex
of the complex  -plane is called compact if one can select from any sequence
-plane is called compact if one can select from any sequence 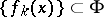 a subsequence converging to an analytic function in
a subsequence converging to an analytic function in 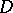 or, what is the same, converging uniformly in the interior of
or, what is the same, converging uniformly in the interior of 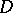 , that is, uniformly converging on any compactum
, that is, uniformly converging on any compactum 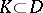 . The compactness principle was formulated by P. Montel in 1927 (see [1]): In order that a family
. The compactness principle was formulated by P. Montel in 1927 (see [1]): In order that a family 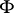 be compact, it is necessary and sufficient that it be uniformly bounded in the interior of
be compact, it is necessary and sufficient that it be uniformly bounded in the interior of  , that is, uniformly bounded on any compactum
, that is, uniformly bounded on any compactum 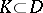 .
.
Let 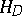 be the complex vector space of holomorphic functions in a domain
be the complex vector space of holomorphic functions in a domain 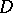 of the space
of the space 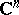 ,
, 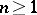 , with the topology of uniform convergence on compacta
, with the topology of uniform convergence on compacta 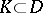 . The compactness principle can be stated in a more abstract form: A closed set
. The compactness principle can be stated in a more abstract form: A closed set 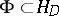 is compact in
is compact in 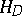 if and only if it is bounded in
if and only if it is bounded in 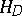 . The notion of a compact family of analytic functions is closely related to that of a normal family. See also Vitali theorem.
. The notion of a compact family of analytic functions is closely related to that of a normal family. See also Vitali theorem.
References
| [1] | P. Montel, "Leçons sur les familles normales de fonctions analytiques et leurs applications" , Gauthier-Villars (1927) |
| [2] | B. Malgrange, "Lectures on the theory of functions of several complex variables" , Tata Inst. (1958) |
Comments
References
| [a1] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) pp. Sect. 86 (Translated from Russian) |
Compactness principle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Compactness_principle&oldid=12245