Covariant

of a tensor 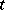on a finite-dimensional vector space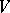

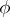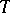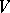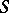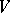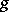A mapping of the space of tensors of a fixed type over into a space of covariant tensors over such that for any non-singular linear transformation of 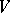and any 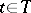. This is the definition of the covariant of a tensor with respect to the general linear group 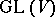. If 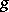is not arbitrary but belongs to a fixed subgroup 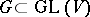, then one obtains the definition of a covariant of a tensor relative to 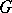, or simply a covariant of .

In coordinate language, a covariant of a tensor on a finite-dimensional vector space is a set of functions

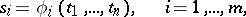of the components of the tensor with the following properties: Under a change of the set of numbers defined by a non-singular linear transformation 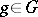, the set of numbers 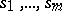changes according to that of a covariant tensor over under the transformation 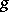. In similar fashion one defines (by considering instead of one tensor 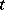a finite collection of tensors) a joint covariant of the system of tensors. If instead, one replaces the covariance condition for the tensor by contravariance, one obtains the notion of a contravariant.

The notion of a covariant arose in the classical theory of invariants and is a special case of the notion of a comitant. The components of any tensor can be regarded as the coefficients of an appropriate form in several contravariant and covariant vectors (that is, vectors of 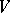and its dual 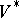, cf. "form associated to a tensor" in the article Tensor on a vector space). Suppose that the form 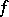corresponds in this manner to the tensor 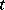and that the form 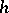corresponds to its covariant . Then 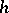if a form of contravariant vectors only. In the classical theory of invariants 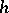was called the covariant of 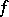. A case that was particularly often considered is when 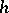is a form in one single contravariant vector. The degree of this form is called the order of the covariant. If the coefficients of are polynomials in the coefficients of , then the highest of the degrees of these polynomials is called the degree of the covariant.

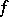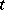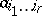Example. Let be a form of a degree , where are the components of a contravariant vector. The form corresponds to a symmetric covariant tensor of valency with components . Let

Then the coefficients of 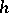are the components of some covariant tensor . The tensor (or the form ) is a covariant of the tensor 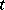(or form ). The form 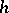is called the Hessian of .

References

[1]	G.B. Gurevich, "Foundations of the theory of algebraic invariants" , Noordhoff (1964) (Translated from Russian)