Gronwall summation method
From Encyclopedia of Mathematics
A method for summing series of numbers or functions, defined by specifying two functions  and
and  satisfying certain conditions. A series
satisfying certain conditions. A series  can be summed by the Gronwall method
can be summed by the Gronwall method  to a sum
to a sum  if
if
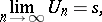 |
where  ,
,  is defined by the expansion
is defined by the expansion
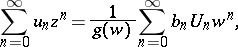 |
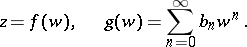 |
The method was introduced by T.H. Gronwall [1] as a generalization of the de la Vallée-Poussin summation method, to which it is converted by
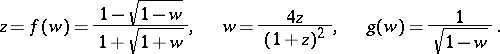 |
If
 |
then the Gronwall summation method becomes one of the Cesàro summation methods.
References
| [1] | T.H. Gronwall, "Summation of series and conformal mapping" Ann. of Math. , 33 : 1 (1932) pp. 101–117 |
How to Cite This Entry:
Gronwall summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gronwall_summation_method&oldid=12127
Gronwall summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gronwall_summation_method&oldid=12127
This article was adapted from an original article by I.I. Volkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article