Ellipse of normal curvature

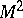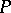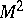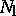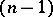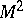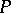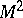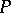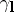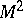A geometrical construction characterizing the distribution of the curvatures at a certain point on a regular surface in the -dimensional Euclidean space . Let be a point on a surface and let be the -dimensional subspace containing the normal space to at and the tangent to at in the direction . The section of by 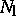is called a normal section at 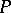. The vector , lying in 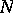, where is the natural parameter on 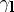, is called the vector of normal curvature of 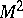in the direction . The end points of the vectors of normal curvature form the ellipse of normal curvature.

For a two-dimensional surface 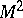with non-zero Gaussian curvature in 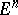to lie in a certain three-dimensional subspace 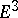it is necessary and sufficient that its ellipse of normal curvature at all points 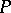degenerates to a segment passing through 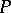(see ).

Similarly one defines the indicatrix of curvature for a submanifold 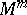of arbitrary dimension 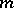. It is an 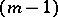-dimensional algebraic surface of order 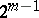. The vectors of normal curvature form a cone which, together with the tangent space to 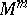, determines a subspace 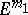, the so-called domain of curvature of 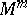at 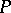. The dimension 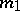of this subspace satisfies

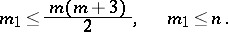Points at which 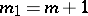are called axial, those at which 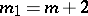— planar, and those at which 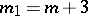— spatial. Sometimes one considers for submanifolds of large codimension the Dupin indicatrix, the construction of which is completely analogous to that of the Dupin indicatrix for a surface in three-dimensional space.

References

[1]	J.A. Schouten, D.J. Struik, "Einführung in die neueren Methoden der Differentialgeometrie" , 2 , Noordhoff (1935)
[2a]	Yu.A. Aminov, "Torsion of two-dimensional surfaces in Euclidean spaces" Ukrain. Geom. Sb. , 17 (1975) pp. 3–14 (In Russian)
[2b]	Yu.A. Aminov, "An analogue of Ricci's condition for a minimal variety in a Riemannian space" Ukrain. Geom. Sb. , 17 (1975) pp. 15–22; 144 (In Russian)

References

[a1]	M. do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976)
[a2]	B. O'Neill, "Elementary differential geometry" , Acad. Press (1966)
[a3]	S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1–2 , Interscience (1969) pp. Chapt. 7
[a4]	M. Spivak, "A comprehensive introduction to differential geometry" , 3 , Publish or Perish pp. 1–5