Characteristic functional

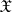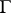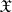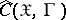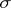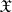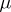An analogue of the concept of a characteristic function; it is used in the infinite-dimensional case. Let be a non-empty set, let be a vector space of real-valued functions defined on and let be the smallest -algebra of subsets of relative to which all functions in are measurable. The characteristic functional of a probability measure given on 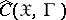is defined as the complex-valued functional 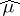on 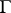given by the equation

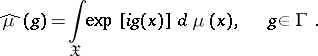From now on the most important and simplest case when 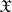is a separable real Banach space and 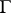is its topological dual 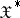is studied. In this case coincides with the 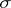-algebra of Borel sets of 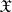. The concept of a characteristic functional for infinite-dimensional Banach spaces was introduced by A.N. Kolmogorov in [1].

The characteristic functional of a random variable 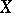with values in 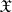is, by definition, that of its probability distribution , .

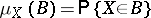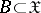Main properties of the characteristic functional:

1) 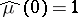and 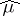is positive definite, i.e. 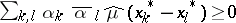for any finite set of complex numbers and elements ;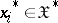

2) 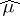is continuous in the strong topology and sequentially continuous in the weak topology of ;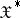

3) ,

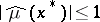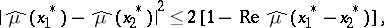where ;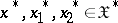

4) 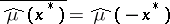; in particular, 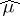takes only real values (and is an even functional) if and only if the measure 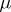is symmetric, that is, 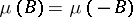, where ;

5) the characteristic functional determines the measure uniquely;

6) the characteristic functional of the convolution of two probability measures (of the sum of two independent random variables) is the product of their characteristic functionals.

In the finite-dimensional case the method of characteristic functionals is based on the theorem about the continuity of the correspondence between measures and their characteristic functionals, and on a theorem concerning the description of the class of characteristic functionals. In the infinite-dimensional case the direct analogues of these theorems do not hold. 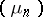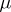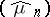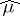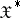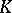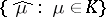If a sequence of probability measures converges weakly to , then converges pointwise to , and this convergence is uniform on bounded subsets of ; if is a weakly relatively-compact family of probability measures on , then the family is equicontinuous in the strong topology of 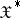. The converse assertions only hold in the finite-dimensional case. However, the conditions of convergence and of weak relative compactness of families of probability measures can be expressed in terms of characteristic functionals (see [2]). Furthermore, in contrast to the finite-dimensional case, not every positive-definite normalized (equal to 1 at the origin) continuous functional is a characteristic functional: continuity in the metric topology is not sufficient. A topology in 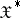is called sufficient, or necessary, if in this topology the continuity of a positive-definite normalized functional is sufficient, or necessary, for it to be the characteristic functional of some probability measure on 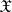. A necessary and sufficient topology is said to be an 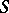-topology. A space 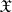is called an 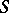-space if there is an 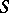-topology on 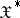. A Hilbert space is an 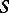-space (see [3]).

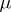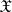The most important characteristic functionals are those of Gaussian measures. A measure in is called a centred Gaussian measure if for all ,

(*)

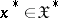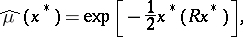where 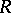, a bounded linear positive operator from 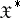into , is the covariance operator of the measure 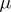, defined by the relation

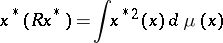(see [4]). In contrast to the finite-dimensional case, not every functional of the form (*) is a characteristic functional: additional restrictions on 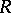are needed, depending on the space 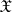. For example, if 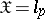, , 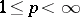then an additional (necessary and sufficient) condition is 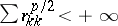, where 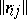is the matrix of the operator 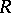in the natural basis (see [5]). In particular, in a Hilbert space the additional condition is that the operator 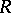be nuclear.

References

[1]	A.N. Kolmogorov, C.R. Acad. Sci. Paris , 200 (1935) pp. 1717–1718
[2]	Yu.V. Prokhorov, "Convergence of random processes and limit theorems in probability theory" Theory Probab. Appl. , 1 (1956) pp. 157–214 Teor. Veroyatnost. i Primen. , 1 : 2 (1956) pp. 177–238
[3]	V.V. Sazonov, "A remark on characteristic functionals" Theory Probab. Appl. , 3 (1958) pp. 188–192 Teor. Veroyatnost. i Primen. , 3 : 2 (1958) pp. 201–205
[4]	N.N. Vakhania, V.I. Tarieladze, S.A. Chobanyan, "Probability distributions on Banach spaces" , Reidel (1987) (Translated from Russian)
[5]	N.N. Vakhania, "Sur les répartitions de probabilités dans les espaces de suites numériques" C.R. Acad. Sci. Paris , 260 (1965) pp. 1560–1562

References

[a1]	N.N. Vakhania, "Probability distributions on linear spaces" , North-Holland (1981) (Translated from Russian)