The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
Let 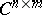 be the set of complex
be the set of complex 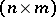 -matrices and
-matrices and 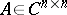 . Let
. Let
be the characteristic polynomial of 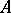 , where
, where 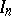 is the
is the 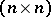 identity matrix. The Cayley–Hamilton theorem says [a2], [a9] that every square matrix satisfies its own characteristic equation, i.e.
identity matrix. The Cayley–Hamilton theorem says [a2], [a9] that every square matrix satisfies its own characteristic equation, i.e.
where  is the zero-matrix.
is the zero-matrix.
The classical Cayley–Hamilton theorem can be extended to rectangle matrices. A matrix 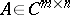 for
for 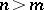 may be written as
may be written as 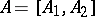 ,
, 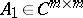 ,
, 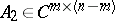 . Let
. Let
Then the matrix  (
( ) satisfies the equation [a8]
) satisfies the equation [a8]
A matrix 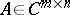 (
(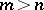 ) may be written as
) may be written as
Let
Then the matrix 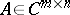 (
(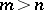 ) satisfies the equation [a8]
) satisfies the equation [a8]
The Cayley–Hamilton theorem can be also extended to block matrices ([a4], [a13], [a15]). Let
 | (a1) |
where  are commutative, i.e.
are commutative, i.e. 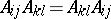 for all
for all 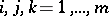 . Let
. Let
be the matrix characteristic polynomial and let 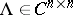 be the matrix (block) eigenvalue of
be the matrix (block) eigenvalue of 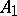 , where
, where 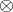 denotes the Kronecker product. The matrix
denotes the Kronecker product. The matrix 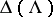 is obtained by developing the determinant of
is obtained by developing the determinant of 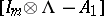 , considering its commuting blocks as elements [a15].
, considering its commuting blocks as elements [a15].
The block matrix (a1) satisfies the equation [a15]
Consider now a rectangular block matrix 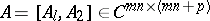 , where
, where  has the form (a1) and
has the form (a1) and 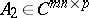 (
(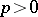 ). The matrix
). The matrix 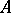 satisfies the equation [a4]
satisfies the equation [a4]
If 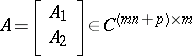 , where
, where 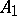 has the form (a1) and
has the form (a1) and 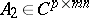 , then
, then
A pair of matrices 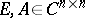 is called regular if
is called regular if 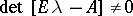 for some
for some 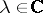 [a10], [a11], [a12]. The pair is called standard if there exist scalars
[a10], [a11], [a12]. The pair is called standard if there exist scalars 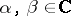 such that
such that 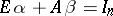 . If the pair
. If the pair 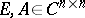 is regular, then the pair
is regular, then the pair
 | (a2) |
is standard. If the pair 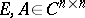 is standard, then it is also commutative (
is standard, then it is also commutative (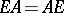 ). Let a pair
). Let a pair 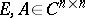 be standard (commutative) and
be standard (commutative) and
Then the pair satisfies the equation [a1]
In a particular case, with 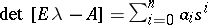 , it follows that
, it follows that 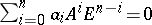 .
.
Let 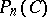 be the set of
be the set of  -order square complex matrices that commute in pairs and let
-order square complex matrices that commute in pairs and let 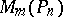 be the set of square matrices partitioned in
be the set of square matrices partitioned in 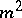 blocks belonging to
blocks belonging to 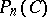 .
.
Consider a standard pair of block matrices 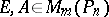 and let the matrix polynomial
and let the matrix polynomial
be its matrix characteristic polynomial. The pair 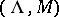 is called the block-eigenvalue pair of the pair
is called the block-eigenvalue pair of the pair 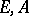 .
.
Then [a6]
The Cayley–Hamilton theorem can be also extended to singular two-dimensional linear systems described by Roesser-type or Fomasini–Marchesini-type models [a3], [a14]. The singular two-dimensional Roesser model is given by
Here, 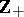 is the set of non-negative integers;
is the set of non-negative integers;  , respectively
, respectively 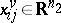 , are the horizontal, respectively vertical, semi-state vector at the point
, are the horizontal, respectively vertical, semi-state vector at the point 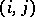 ;
;  is the input vector;
is the input vector; 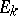 ,
, 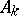 (
(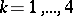 ) and
) and 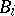 (
(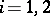 ) have dimensions compatible with
) have dimensions compatible with 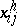 and
and 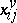 ; and
; and
may be singular. The characteristic polynomial has the form
and the transition matrices 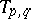 ,
, 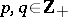 , are defined by
, are defined by
If 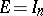 ,
, 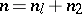 (the standard Roesser model), then the transition matrices
(the standard Roesser model), then the transition matrices 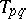 may be computed recursively, using the formula
may be computed recursively, using the formula  , where
, where 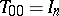 ,
,
The matrices 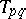 satisfy the equation [a3]
satisfy the equation [a3]
The singular two-dimensional Fornasini–Marchesini model is given by
where 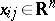 is the local semi-vector at the point
is the local semi-vector at the point 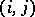 ,
, 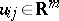 is the input vector,
is the input vector, 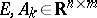 and
and 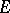 is possibly singular. The characteristic polynomial has the form
is possibly singular. The characteristic polynomial has the form
and the transition matrices 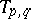 ,
, 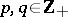 , are defined by
, are defined by
The matrices 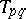 satisfy the equation
satisfy the equation
The theorems may be also extended to two-dimensional continuous-discrete linear systems [a5].
References
| [a1] | F.R. Chang, C.N. Chen, "The generalized Cayley–Hamilton theorem for standard pencils" Systems and Control Lett. , 18 (1992) pp. 179–182 |
| [a2] | F.R. Gantmacher, "The theory of matrices" , 2 , Chelsea (1974) |
| [a3] | T. Kaczorek, "Linear control systems" , I–II , Research Studies Press (1992/93) |
| [a4] | T. Kaczorek, "An extension of the Cayley–Hamilton theorem for non-square blocks matrices and computation of the left and right inverses of matrices" Bull. Polon. Acad. Sci. Techn. , 43 : 1 (1995) pp. 49–56 |
| [a5] | T. Kaczorek, "Extensions of the Cayley Hamilton theorem for  -D continuous discrete linear systems" Appl. Math. and Comput. Sci. , 4 : 4 (1994) pp. 507–515 -D continuous discrete linear systems" Appl. Math. and Comput. Sci. , 4 : 4 (1994) pp. 507–515 |
| [a6] | T. Kaczorek, "An extension of the Cayley–Hamilton theorem for a standard pair of block matrices" Appl. Math. and Comput. Sci. , 8 : 3 (1998) pp. 511–516 |
| [a7] | T. Kaczorek, "An extension of Cayley–Hamillon theorem for singular  -D linear systems with non-square matrices" Bull. Polon. Acad. Sci. Techn. , 43 : 1 (1995) pp. 39–48 -D linear systems with non-square matrices" Bull. Polon. Acad. Sci. Techn. , 43 : 1 (1995) pp. 39–48 |
| [a8] | T. Kaczorek, "Generalizations of the Cayley–Hamilton theorem for nonsquare matrices" Prace Sem. Podstaw Elektrotechnik. i Teor. Obwodów , XVIII–SPETO (1995) pp. 77–83 |
| [a9] | P. Lancaster, "Theory of matrices" , Acad. Press (1969) |
| [a10] | F.L. Lewis, "Cayley--Hamilton theorem and Fadeev's method for the matrix pencil  " , Proc. 22nd IEEE Conf Decision Control (1982) pp. 1282–1288 " , Proc. 22nd IEEE Conf Decision Control (1982) pp. 1282–1288 |
| [a11] | F.L. Lewis, "Further remarks on the Cayley–Hamilton theorem and Leverrie's method for the matrix pencil 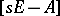 " IEEE Trans. Automat. Control , 31 (1986) pp. 869–870 " IEEE Trans. Automat. Control , 31 (1986) pp. 869–870 |
| [a12] | B.G. Mertzios, M.A. Christodoulous, "On the generalized Cayley–Hamilton theorem" IEEE Trans. Automat. Control , 31 (1986) pp. 156–157 |
| [a13] | N.M. Smart, S. Barnett, "The algebra of matrices in  -dimensional systems" Math. Control Inform. , 6 (1989) pp. 121–133 -dimensional systems" Math. Control Inform. , 6 (1989) pp. 121–133 |
| [a14] | N.J. Theodoru, "A Hamilton theorem" IEEE Trans. Automat. Control , AC–34 : 5 (1989) pp. 563–565 |
| [a15] | J. Victoria, "A block-Cayley–Hamilton theorem" Bull. Math. Soc. Sci. Math. Roum. , 26 : 1 (1982) pp. 93–97 |
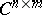 be the set of complex
be the set of complex 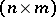 -matrices and
-matrices and 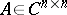 . Let
. Let
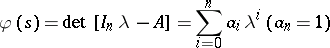
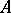 , where
, where 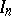 is the
is the 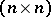 identity matrix. The Cayley–Hamilton theorem says [a2], [a9] that every square matrix satisfies its own characteristic equation, i.e.
identity matrix. The Cayley–Hamilton theorem says [a2], [a9] that every square matrix satisfies its own characteristic equation, i.e.
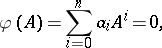
 is the zero-matrix.
is the zero-matrix.
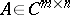 for
for 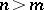 may be written as
may be written as 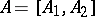 ,
, 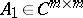 ,
, 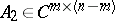 . Let
. Let
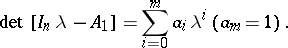
 (
( ) satisfies the equation [a8]
) satisfies the equation [a8]
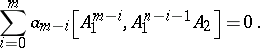
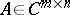 (
(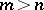 ) may be written as
) may be written as
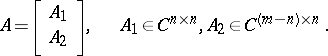
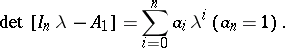
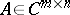 (
(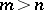 ) satisfies the equation [a8]
) satisfies the equation [a8]
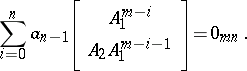

 are commutative, i.e.
are commutative, i.e. 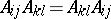 for all
for all 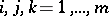 . Let
. Let
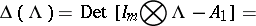
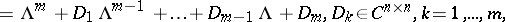
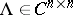 be the matrix (block) eigenvalue of
be the matrix (block) eigenvalue of 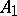 , where
, where 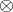 denotes the Kronecker product. The matrix
denotes the Kronecker product. The matrix 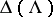 is obtained by developing the determinant of
is obtained by developing the determinant of 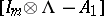 , considering its commuting blocks as elements [a15].
, considering its commuting blocks as elements [a15].
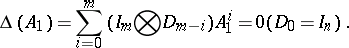
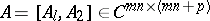 , where
, where  has the form (a1) and
has the form (a1) and 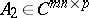 (
(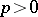 ). The matrix
). The matrix 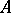 satisfies the equation [a4]
satisfies the equation [a4]
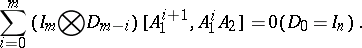
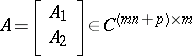 , where
, where 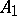 has the form (a1) and
has the form (a1) and 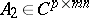 , then
, then
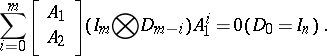
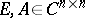 is called regular if
is called regular if 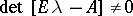 for some
for some 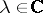 [a10], [a11], [a12]. The pair is called standard if there exist scalars
[a10], [a11], [a12]. The pair is called standard if there exist scalars 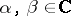 such that
such that 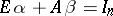 . If the pair
. If the pair 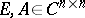 is regular, then the pair
is regular, then the pair

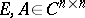 is standard, then it is also commutative (
is standard, then it is also commutative (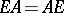 ). Let a pair
). Let a pair 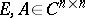 be standard (commutative) and
be standard (commutative) and
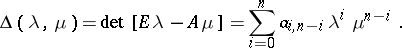
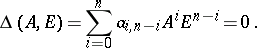
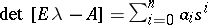 , it follows that
, it follows that 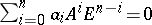 .
.
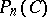 be the set of
be the set of  -order square complex matrices that commute in pairs and let
-order square complex matrices that commute in pairs and let 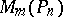 be the set of square matrices partitioned in
be the set of square matrices partitioned in 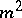 blocks belonging to
blocks belonging to 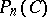 .
.
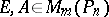 and let the matrix polynomial
and let the matrix polynomial
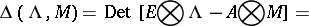
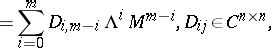
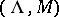 is called the block-eigenvalue pair of the pair
is called the block-eigenvalue pair of the pair 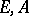 .
.
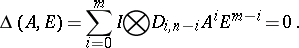

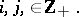
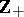 is the set of non-negative integers;
is the set of non-negative integers;  , respectively
, respectively 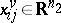 , are the horizontal, respectively vertical, semi-state vector at the point
, are the horizontal, respectively vertical, semi-state vector at the point 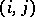 ;
;  is the input vector;
is the input vector; 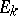 ,
, 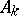 (
(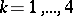 ) and
) and 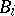 (
(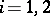 ) have dimensions compatible with
) have dimensions compatible with 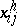 and
and 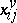 ; and
; and
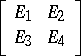
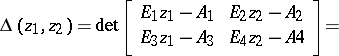
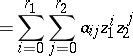
 ,
, 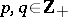 , are defined by
, are defined by
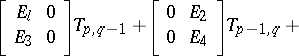
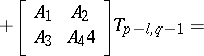
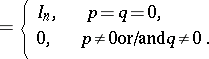
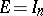 ,
, 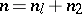 (the standard Roesser model), then the transition matrices
(the standard Roesser model), then the transition matrices 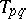 may be computed recursively, using the formula
may be computed recursively, using the formula  , where
, where 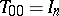 ,
,
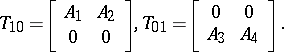
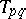 satisfy the equation [a3]
satisfy the equation [a3]
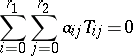
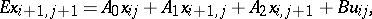
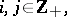
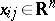 is the local semi-vector at the point
is the local semi-vector at the point 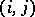 ,
, 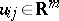 is the input vector,
is the input vector, 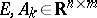 and
and 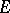 is possibly singular. The characteristic polynomial has the form
is possibly singular. The characteristic polynomial has the form
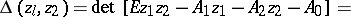
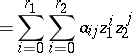
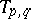 ,
, 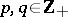 , are defined by
, are defined by

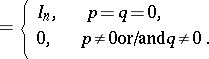
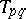 satisfy the equation
satisfy the equation
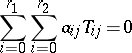
 -D continuous discrete linear systems" Appl. Math. and Comput. Sci. , 4 : 4 (1994) pp. 507–515
-D continuous discrete linear systems" Appl. Math. and Comput. Sci. , 4 : 4 (1994) pp. 507–515 -D linear systems with non-square matrices" Bull. Polon. Acad. Sci. Techn. , 43 : 1 (1995) pp. 39–48
-D linear systems with non-square matrices" Bull. Polon. Acad. Sci. Techn. , 43 : 1 (1995) pp. 39–48 " , Proc. 22nd IEEE Conf Decision Control (1982) pp. 1282–1288
" , Proc. 22nd IEEE Conf Decision Control (1982) pp. 1282–1288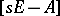 " IEEE Trans. Automat. Control , 31 (1986) pp. 869–870
" IEEE Trans. Automat. Control , 31 (1986) pp. 869–870 -dimensional systems" Math. Control Inform. , 6 (1989) pp. 121–133
-dimensional systems" Math. Control Inform. , 6 (1989) pp. 121–133