Fully-characteristic congruence
A congruence 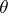 of an algebraic system
of an algebraic system 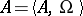 which is invariant under any endomorphism
which is invariant under any endomorphism 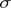 of this system, i.e. it follows from
of this system, i.e. it follows from 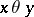 that
that 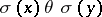 (
( ). The fully-characteristic congruences of an algebraic system
). The fully-characteristic congruences of an algebraic system 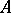 form under inclusion a complete sublattice
form under inclusion a complete sublattice 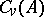 of the lattice
of the lattice 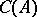 of all congruences of
of all congruences of 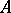 . If
. If 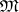 is a variety of
is a variety of  -systems and if
-systems and if 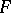 is a free algebra in
is a free algebra in 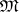 on a countably infinite set of generators, the lattice
on a countably infinite set of generators, the lattice 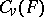 of fully-characteristic congruences of the system
of fully-characteristic congruences of the system 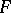 is dually isomorphic to the lattice
is dually isomorphic to the lattice 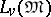 of all subvarieties of
of all subvarieties of 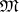 . Any congruence
. Any congruence 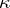 of an
of an  -algebra
-algebra 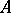 with a finite number of generators, of finite index in
with a finite number of generators, of finite index in 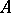 (i.e. with a finite number of congruence classes
(i.e. with a finite number of congruence classes 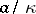 ,
, 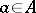 ), contains a fully-characteristic congruence
), contains a fully-characteristic congruence 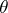 of
of 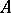 which also has finite index in
which also has finite index in 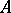 .
.
References
| [1] | A.I. Mal'tsev, "Algebraic systems" , Springer (1973) (Translated from Russian) |
Comments
Fully-characteristic congruences are also called fully-invariant congruences.
References
| [a1] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
Fully-characteristic congruence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fully-characteristic_congruence&oldid=11764