Serial subgroup

Let be a subgroup of a group 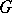. A series of subgroups between 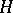and 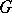, or, more briefly, a series between 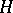and 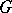, is a set of subgroups of ,

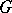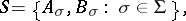where 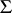is a linearly ordered set, such that

i) 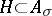, 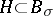for all ;

ii) ;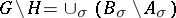

iii) 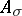is a normal subgroup of ;

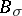iv) 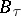is a subgroup o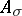f if .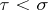

It follows that for all ,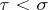

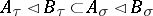and

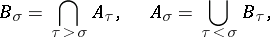and for a finite series, indexed by 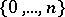, hence

A subgroup 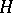is called serial if there is a series of subgroups between 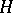and . If 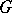is finite, a subgroup 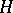is serial if and only if it is a subnormal subgroup. A subgroup 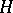is called an ascendant subgroup in 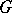if there is an ascending series of subgroups between 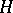and 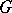, that is, a series whose index set 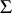is well-ordered.

References

[a1]	D.J.S. Robinson, "Finiteness condition and generalized soluble groups" , 1 , Springer (1972) pp. Chapt. 1