Closed-graph theorem
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
Let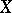 
and 
be complete metric linear spaces with translation-invariant metrics, i.e.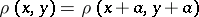 
, 
(similarly for 
), and let 
be a linear operator from 
to 
. If the graph 
of this operator is a closed subset of the Cartesian product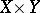 
, then 
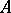is continuous. The closed-graph theorem has various generalizations; for example: a linear mapping with closed graph from a separable barrelled space into a perfectly-complete space is continuous. Closely related theorems are the open-mapping theorem and Banach's homeomorphism theorem.
References
| [1] | W. Rudin, "Functional analysis" , McGraw-Hill (1979) |
| [2] | A.P. Robertson, W.S. Robertson, "Topological vector spaces" , Cambridge Univ. Press (1964) |
Comments
Cf. also Open-mapping theorem (also for the Banach homeomorphism theorem).
How to Cite This Entry:
Closed-graph theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Closed-graph_theorem&oldid=11648
Closed-graph theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Closed-graph_theorem&oldid=11648
This article was adapted from an original article by V.I. Sobolev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article