Weak extremum
A minimal or maximal value 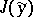 , attained by a functional
, attained by a functional 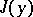 on a curve
on a curve 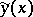 ,
, 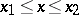 , for which one of the following inequalities holds:
, for which one of the following inequalities holds:
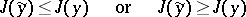 |
for all comparison curves 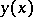 situated in an
situated in an  -proximity neighbourhood of
-proximity neighbourhood of 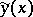 with respect to both
with respect to both 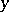 and its derivative:
and its derivative:
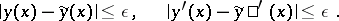 |
The curves 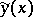 ,
, 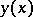 must satisfy the prescribed boundary conditions.
must satisfy the prescribed boundary conditions.
Since the maximization of  is equivalent to the minimization of
is equivalent to the minimization of 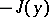 , one often speaks of a weak minimum instead of a weak extremum. The term "weak" emphasizes the fact that the comparison curves
, one often speaks of a weak minimum instead of a weak extremum. The term "weak" emphasizes the fact that the comparison curves 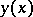 satisfy the
satisfy the  -proximity condition not only on the ordinate but also on its derivative (in contrast to the case of a strong extremum, where the
-proximity condition not only on the ordinate but also on its derivative (in contrast to the case of a strong extremum, where the  -proximity of
-proximity of 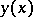 and
and 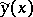 refer only to the former).
refer only to the former).
By definition, a weak minimum is a weak relative minimum, since the latter gives a minimum among the members of a subset of the whole class of admissible comparison curves  for which
for which 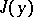 makes sense. However, for the sake of brevity, the term "weak minimum" is used for both.
makes sense. However, for the sake of brevity, the term "weak minimum" is used for both.
References
| [1] | M.A. Lavrent'ev, L.A. Lyusternik, "A course in variational calculus" , Moscow-Leningrad (1950) (In Russian) |
| [2] | V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) (Translated from Russian) |
Weak extremum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weak_extremum&oldid=11623