Well-founded relation

well-founded partial order

A (partial order) relation on a set 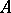is called well-founded, or recursive, if every non-empty subset of 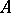has a least element with respect to this relation. Thus, a total order on a set 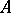(cf. Totally ordered set) that is well-founded makes 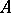a well-ordered set.

A relati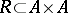on on 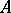is well-founded if and only if for any set 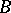and function 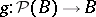there is a unique function 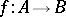such that the following diagram commutes (cf. [a1]):

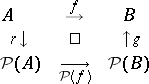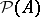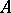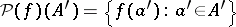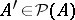Here, is the set of all subsets of , for and 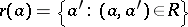. In this form well-foundedness is defined in any elementary topos.

References

[a1]	G. Osius, "Categorical set theory: a characterization of the category of sets" J. Pure Appl. Algebra , 4 (1974) pp. 79–119
[a2]	P. Odifreddi, "Classical recursion theory" , North-Holland (1989) pp. Chapt. II; esp. pp. 199ff
[a3]	R.I. Goldblatt, "Topoi: the categorical analysis of logic" , North-Holland (1984) pp. 318ff