Stepanov almost-periodic functions
A class  of functions that are measurable and summable together with their
of functions that are measurable and summable together with their 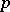 -th power
-th power 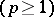 on every finite interval
on every finite interval  and that can be approximated in the metric of the Stepanov space (see below) by finite sums
and that can be approximated in the metric of the Stepanov space (see below) by finite sums
 |
where  are complex coefficients and
are complex coefficients and 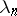 are real numbers. The distance in the Stepanov space is defined by the formula
are real numbers. The distance in the Stepanov space is defined by the formula
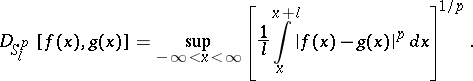 |
Functions of the class 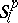 can also be defined using the concept of an almost-period.
can also be defined using the concept of an almost-period.
Functions of the class 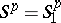 possess a number of properties also possessed by Bohr almost-periodic functions. For example, functions of the class
possess a number of properties also possessed by Bohr almost-periodic functions. For example, functions of the class 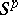 are bounded and uniformly continuous (in the metric
are bounded and uniformly continuous (in the metric 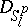 ), the limit
), the limit  of a convergent sequence of Stepanov almost-periodic functions
of a convergent sequence of Stepanov almost-periodic functions  (in the metric of
(in the metric of  ) belongs to
) belongs to 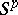 . If a function in
. If a function in 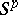 is uniformly continuous (in the ordinary sense) on the whole real axis, then it is a Bohr almost-periodic function. Introduced by V.V. Stepanov [1].
is uniformly continuous (in the ordinary sense) on the whole real axis, then it is a Bohr almost-periodic function. Introduced by V.V. Stepanov [1].
References
| [1] | W. [V.V. Stepanov] Stepanoff, "Sur quelques généralisations des fonctions presque périodiques" C.R. Acad. Sci. Paris , 181 (1925) pp. 90–92 |
Comments
See also Almost-periodic function.
The different spaces  , each with its metric
, each with its metric 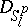 , are topologically equivalent.
, are topologically equivalent.
References
| [a1] | W. [V.V. Stepanov] Stepanoff, "Ueber einige Verallgemeinerungen der fastperiodischen Funktionen" Math. Ann. , 45 (1925) pp. 473–498 |
Stepanov almost-periodic functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stepanov_almost-periodic_functions&oldid=11586