of one random variable 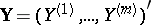 on another
on another 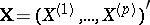
An 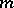 -dimensional vector form, linear in
-dimensional vector form, linear in  , supposed to be the conditional mean (given
, supposed to be the conditional mean (given 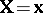 ) of the random vector
) of the random vector 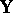 . The corresponding equations
. The corresponding equations
 | (*) |
are called the linear regression equations of 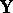 on
on 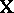 , and the parameters
, and the parameters 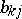 are called the regression coefficients (see also Regression),
are called the regression coefficients (see also Regression), 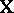 is an observable parameter (not necessarily random), on which the mean of the resulting function (response)
is an observable parameter (not necessarily random), on which the mean of the resulting function (response) 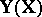 under investigation depends.
under investigation depends.
In addition, the linear regression of 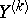 on
on 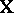 is frequently also understood to be the "best" (in a well-defined sense) linear approximation of
is frequently also understood to be the "best" (in a well-defined sense) linear approximation of 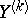 by means of
by means of 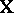 , or even the result of the best (in a well-defined sense) smoothing of a system of experimental points ( "observations" )
, or even the result of the best (in a well-defined sense) smoothing of a system of experimental points ( "observations" ) 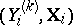 ,
, 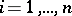 , by means of a hyperplane in the space
, by means of a hyperplane in the space 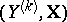 , in situations when the interpretation of these points as samples from a corresponding general population need not be allowable. With such a definition one has to distinguish different versions of linear regression, depending on the choice of the method of computing the errors of the linear approximation of
, in situations when the interpretation of these points as samples from a corresponding general population need not be allowable. With such a definition one has to distinguish different versions of linear regression, depending on the choice of the method of computing the errors of the linear approximation of 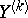 by means of
by means of 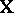 (or depending on the actual choice of a criterion for the amount of smoothing). The most widespread criteria for the quality of the approximation of
(or depending on the actual choice of a criterion for the amount of smoothing). The most widespread criteria for the quality of the approximation of 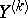 by means of linear combinations of
by means of linear combinations of 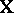 (linear smoothing of the points
(linear smoothing of the points 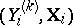 ) are:
) are:
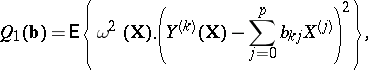 |
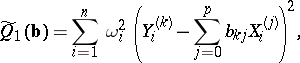 |
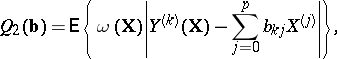 |
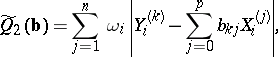 |
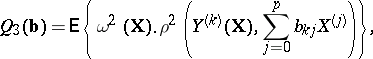 |
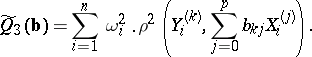 |
In these relations the choice of "weights" 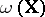 or
or 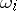 depends on the nature of the actual scheme under investigation. For example, if the
depends on the nature of the actual scheme under investigation. For example, if the 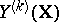 are interpreted as random variables with known variances
are interpreted as random variables with known variances 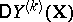 (or with known estimates of them), then
(or with known estimates of them), then 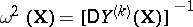 . In the last two criteria the "discrepancies" of the approximation or the smoothing are measured by the distances
. In the last two criteria the "discrepancies" of the approximation or the smoothing are measured by the distances 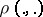 from
from 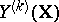 or
or  to the required hyperplane of regression. If the coefficients
to the required hyperplane of regression. If the coefficients 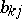 are determined by minimizing the quantities
are determined by minimizing the quantities  or
or 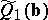 , then the linear regression is said to be least squares or
, then the linear regression is said to be least squares or 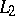 ; if the criteria
; if the criteria 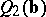 and
and 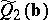 are used, the linear regression is said to be minimal absolute deviations or
are used, the linear regression is said to be minimal absolute deviations or 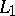 ; if the criteria
; if the criteria 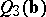 and
and 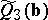 are used, it is said to be minimum
are used, it is said to be minimum 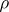 -distance.
-distance.
In certain cases, linear regression in the classical sense (*) is the same as linear regression defined by using functionals of the type 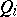 . Thus, if the vector
. Thus, if the vector 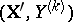 is subject to a multi-dimensional normal law, then the regression of
is subject to a multi-dimensional normal law, then the regression of 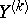 on
on 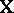 in the sense of (*) is linear and is the same as least squares or minimum mean squares linear regression (for
in the sense of (*) is linear and is the same as least squares or minimum mean squares linear regression (for 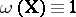 ).
).
References
| [1] | Yu.V. Linnik, "Methode der kleinste Quadraten in moderner Darstellung" , Deutsch. Verlag Wissenschaft. (1961) (Translated from Russian) |
| [2] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [3] | M.G. Kendall, A. Stuart, "The advanced theory of statistics" , 2. Inference and relationship , Macmillan (1979) |
| [4] | C.R. Rao, "Linear statistical inference and its applications" , Wiley (1965) |
How to Cite This Entry:
Linear regression. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_regression&oldid=11531
This article was adapted from an original article by S.A. Aivazyan (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article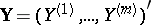 on another
on another 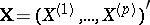
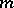 -dimensional vector form, linear in
-dimensional vector form, linear in  , supposed to be the conditional mean (given
, supposed to be the conditional mean (given 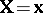 ) of the random vector
) of the random vector 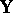 . The corresponding equations
. The corresponding equations

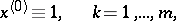
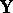 on
on 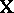 , and the parameters
, and the parameters 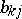 are called the regression coefficients (see also Regression),
are called the regression coefficients (see also Regression), 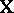 is an observable parameter (not necessarily random), on which the mean of the resulting function (response)
is an observable parameter (not necessarily random), on which the mean of the resulting function (response) 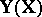 under investigation depends.
under investigation depends.
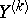 on
on 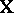 is frequently also understood to be the "best" (in a well-defined sense) linear approximation of
is frequently also understood to be the "best" (in a well-defined sense) linear approximation of 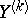 by means of
by means of 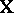 , or even the result of the best (in a well-defined sense) smoothing of a system of experimental points ( "observations" )
, or even the result of the best (in a well-defined sense) smoothing of a system of experimental points ( "observations" ) 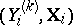 ,
, 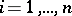 , by means of a hyperplane in the space
, by means of a hyperplane in the space 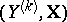 , in situations when the interpretation of these points as samples from a corresponding general population need not be allowable. With such a definition one has to distinguish different versions of linear regression, depending on the choice of the method of computing the errors of the linear approximation of
, in situations when the interpretation of these points as samples from a corresponding general population need not be allowable. With such a definition one has to distinguish different versions of linear regression, depending on the choice of the method of computing the errors of the linear approximation of 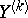 by means of
by means of 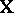 (or depending on the actual choice of a criterion for the amount of smoothing). The most widespread criteria for the quality of the approximation of
(or depending on the actual choice of a criterion for the amount of smoothing). The most widespread criteria for the quality of the approximation of 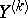 by means of linear combinations of
by means of linear combinations of 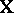 (linear smoothing of the points
(linear smoothing of the points 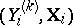 ) are:
) are:
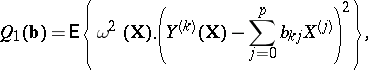
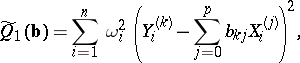
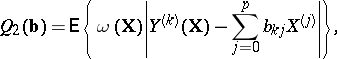
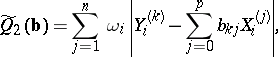
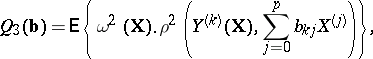
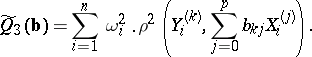
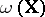 or
or 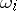 depends on the nature of the actual scheme under investigation. For example, if the
depends on the nature of the actual scheme under investigation. For example, if the 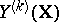 are interpreted as random variables with known variances
are interpreted as random variables with known variances 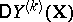 (or with known estimates of them), then
(or with known estimates of them), then 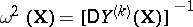 . In the last two criteria the "discrepancies" of the approximation or the smoothing are measured by the distances
. In the last two criteria the "discrepancies" of the approximation or the smoothing are measured by the distances 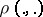 from
from 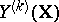 or
or  to the required hyperplane of regression. If the coefficients
to the required hyperplane of regression. If the coefficients 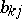 are determined by minimizing the quantities
are determined by minimizing the quantities  or
or 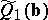 , then the linear regression is said to be least squares or
, then the linear regression is said to be least squares or 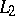 ; if the criteria
; if the criteria 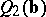 and
and 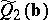 are used, the linear regression is said to be minimal absolute deviations or
are used, the linear regression is said to be minimal absolute deviations or 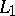 ; if the criteria
; if the criteria 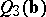 and
and 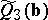 are used, it is said to be minimum
are used, it is said to be minimum 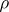 -distance.
-distance.
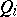 . Thus, if the vector
. Thus, if the vector 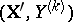 is subject to a multi-dimensional normal law, then the regression of
is subject to a multi-dimensional normal law, then the regression of 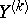 on
on 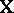 in the sense of (*) is linear and is the same as least squares or minimum mean squares linear regression (for
in the sense of (*) is linear and is the same as least squares or minimum mean squares linear regression (for 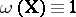 ).
).