Bochner almost-periodic functions

Functions equivalent to Bohr almost-periodic functions; defined by S. Bochner [1]. A function 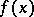which is continuous in the interval 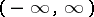is said to be a Bochner almost-periodic function if the family of functions 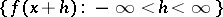is compact in the sense of uniform convergence on 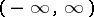, i.e. if it is possible to select from each infinite sequence , 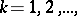a subsequence which converges uniformly to 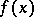on 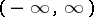. Bochner's definition is extensively employed in the theory of almost-periodic functions; in particular, it serves as the starting point in abstract generalizations of the concept of almost-periodicity.

References

[1]	S. Bochner, "Beiträge zur Theorie der fastperiodischen Funktionen I, Funktionen einer Variablen" Math. Ann. , 96 (1927) pp. 119–147
[2]	B.M. Levitan, "Almost-periodic functions" , Moscow (1953) (In Russian)

References

[a1]	W. Maak, "Fastperiodische Funktionen" , Springer (1967)
[a2]	L. Amerio, G. Prouse, "Almost-periodic functions and functional equations" , v. Nostrand (1971)