Hamilton operator

nabla operator, -operator, Hamiltonian

A symbolic first-order differential operator, used for the notation of one of the principal differential operations of vector analysis. In a rectangular Cartesian coordinate system with unit vectors , the Hamilton operator has the form

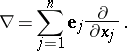The application of the Hamilton operator to a scalar function 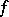, which is understood as multiplication of the "vector" by the scalar 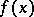, yields the gradient of :

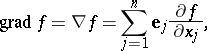i.e. the vector with components .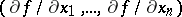

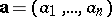The scalar product of with a field vector yields the divergence of :

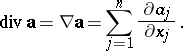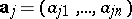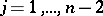The vector product of with the vectors , , yields the curl (rotation, abbreviated by rot) of the fields 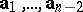, i.e. the vector

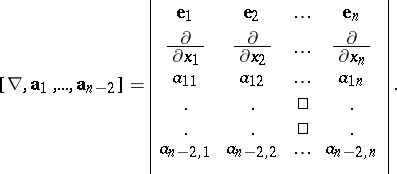If ,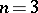

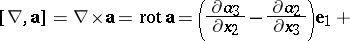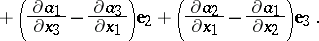The scalar square of the Hamilton operator yields the Laplace operator:

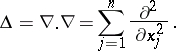The following relations are valid:

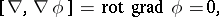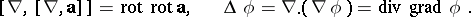The Hamilton operator was introduced by W. Hamilton [1].

References

[1]	W.R. Hamilton, "Lectures on quaternions" , Dublin (1853)

Comments

See also Vector calculus.

References

[a1]	D.E. Rutherford, "Vector mechanics" , Oliver & Boyd (1949)
[a2]	T.M. Apostol, "Calculus" , 1–2 , Blaisdell (1964)
[a3]	H. Holman, H. Rummler, "Alternierende Differentialformen" , B.I. Wissenschaftsverlag Mannheim (1972)