Singular point, index of a
From Encyclopedia of Mathematics
One of the basic characteristics of an isolated singular point of a vector field. Let a vector field  be defined on
be defined on 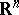 , and let
, and let 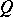 be a sphere of small radius surrounding a singular point
be a sphere of small radius surrounding a singular point 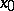 such that
such that  . The degree of the mapping (cf. Degree of a mapping)
. The degree of the mapping (cf. Degree of a mapping)
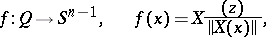 |
is then called the index, 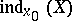 , of the singular point
, of the singular point 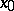 of the vector field
of the vector field  , i.e.
, i.e.
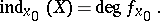 |
If 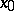 is non-degenerate, then
is non-degenerate, then
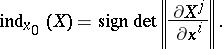 |
Comments
See also Poincaré theorem; Rotation of a vector field.
References
| [a1] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
| [a2] | J.A. Thorpe, "Elementary topics in differential geometry" , Springer (1979) |
| [a3] | C. Conley, E. Zehnder, "Morse type index theory for flows and periodic solutions of Hamiltonian equations" Comm. Pure Appl. Math. , 37 (1984) pp. 207–253 |
| [a4] | K.P. Rybakovskii, "The homotopy index and partial differential equations" , Springer (1987) (Translated from Russian) |
How to Cite This Entry:
Singular point, index of a. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Singular_point,_index_of_a&oldid=11420
Singular point, index of a. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Singular_point,_index_of_a&oldid=11420
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article