Idèle
An invertible element of the ring of adèles (cf. Adèle). The set of all idèles forms a group under multiplication, called the idèle group. The elements of the idèle group of the field of rational numbers are sequences of the form
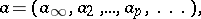 |
where 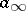 is a non-zero real number,
is a non-zero real number, 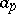 is a non-zero
is a non-zero 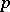 -adic number,
-adic number, 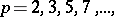 and
and 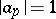 for all but finitely many
for all but finitely many 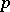 (here
(here 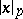 is the
is the  -adic norm). A sequence of idèles
-adic norm). A sequence of idèles
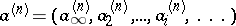 |
is said to converge to an idèle  if it converges to
if it converges to  componentwise and if there exists an
componentwise and if there exists an 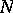 such that
such that 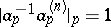 for
for 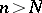 and all
and all  . The idèle group is a locally compact topological group in this topology. The idèle group of an arbitrary number field is constructed in an analogous way.
. The idèle group is a locally compact topological group in this topology. The idèle group of an arbitrary number field is constructed in an analogous way.
The multiplicative group of the field of rational numbers is isomorphically imbedded in the idèle group of this field. Every rational number 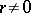 is associated with the sequence
is associated with the sequence
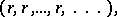 |
which is an idèle. Such an idèle is said to be a principal idèle. The subgroup consisting of all principal idèles is a discrete subgroup of the idèle group.
The concepts of an idèle and an adèle were introduced by C. Chevalley in 1936 for the purposes of algebraic number theory. The new language proved useful in the study of arithmetic aspects of the theory of algebraic groups. To those ends, A. Weil generalized the definitions of an adèle and an idèle to the case of an arbitrary linear algebraic group defined over a number field.
References
| [1] | A. Weil, "Basic number theory" , Springer (1973) |
| [2] | J.W.S. Cassels (ed.) A. Fröhlich (ed.) , Algebraic number theory , Acad. Press (1986) |
Comments
Let 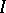 be an index set and for each
be an index set and for each 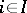 let there be given a locally compact topological ring or group
let there be given a locally compact topological ring or group 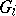 and an open compact subring or subgroup
and an open compact subring or subgroup 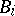 . The restricted direct product
. The restricted direct product 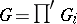 of the
of the 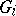 with respect to the
with respect to the 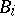 consists of all families
consists of all families 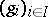 such that
such that 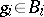 for all but finitely many
for all but finitely many 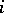 .
. 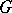 becomes a locally compact group (ring) by taking as a basis of open neighbourhoods of the identity (zero) the sets
becomes a locally compact group (ring) by taking as a basis of open neighbourhoods of the identity (zero) the sets  with
with 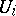 open in
open in 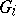 for all
for all 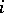 and
and 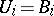 for all but finitely many
for all but finitely many 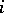 . For each finite set
. For each finite set 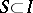 let
let 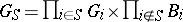 . Then
. Then 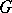 is the union (direct limit) of the
is the union (direct limit) of the 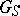 .
.
Now let 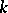 be a number field (or, more generally, a global field). Let
be a number field (or, more generally, a global field). Let 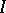 be the set of all prime divisors of
be the set of all prime divisors of 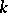 (both finite and infinite ones). For each
(both finite and infinite ones). For each 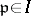 let
let 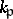 be the completion of
be the completion of 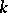 with respect to the norm of
with respect to the norm of 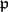 , and let
, and let 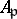 be the ring of integers of
be the ring of integers of 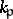 . (Set
. (Set 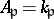 if
if 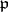 is infinite.) Then the restricted product of the
is infinite.) Then the restricted product of the 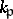 with respect to the
with respect to the 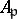 is the ring of adèles
is the ring of adèles 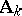 of
of 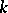 .
.
Now for each 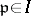 let
let 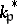 be the group of non-zero elements of
be the group of non-zero elements of 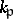 and let
and let 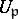 be the group of units of
be the group of units of 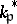 (if
(if 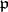 is infinite take
is infinite take 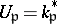 ). The restricted product of the
). The restricted product of the 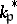 with respect to the
with respect to the 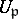 is the group of idèles of
is the group of idèles of 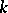 . As a set the group of idèles
. As a set the group of idèles 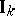 is the set of invertible elements of
is the set of invertible elements of 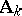 . But the topology on
. But the topology on 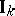 is stronger than that induced by
is stronger than that induced by 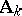 .
.
The quotient of 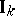 by the diagonal subgroup
by the diagonal subgroup 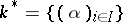 of principal idèles is called the idèle class group; it is important in class field theory.
of principal idèles is called the idèle class group; it is important in class field theory.
The name idèle derives from ideal element. This got abbreviated id.el., which, pronounced in French, gave rise to idèle.
Idèle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Id%C3%A8le&oldid=11409