Conjugate directions
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A pair of directions emanating from a point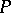 
on a surface 
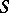such that the straight lines containing them are conjugate diameters of the Dupin indicatrix of 
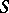at 
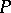. In order that the directions 
, 
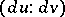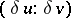at a point 
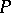on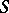 
be conjugate, it is necessary and sufficient that the following condition holds
 |
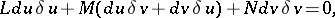where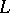 
, 
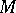and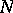 
are the coefficients of the second fundamental form of 
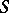evaluated at 
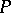. Example: a principal direction.
References
| [1] | A.V. Pogorelov, "Differential geometry" , Noordhoff (1959) (Translated from Russian) |
Comments
References
| [a1] | W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , 1 , Springer (1973) |
| [a2] | C.C. Hsiung, "A first course in differential geometry" , Wiley (1981) pp. Chapt. 3, Sect. 4 |
How to Cite This Entry:
Conjugate directions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conjugate_directions&oldid=11253
Conjugate directions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conjugate_directions&oldid=11253
This article was adapted from an original article by E.V. Shikin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article