Basic set

of a linear system

The set of points of an algebraic variety (or of a scheme) 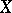which belong to all the divisors of the movable part of the given linear system 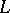on .

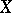Example. Let

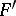be a pencil of -th order curves on the projective plane. The basic set of this pencil then consists of the set of common zeros of the forms and 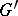, where

and 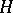is the greatest common divisor of the forms 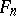and .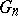

If 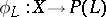is the rational mapping defined by 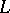, then the basic set of 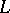is the set of points of indeterminacy of 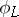. A basic set has the structure of a closed subscheme 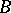in 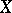, defined as the intersection of all divisors of the movable part of the linear system. The removal of the points of indeterminacy of 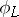can be reduced to the trivialization of the coherent sheaf of ideals defining the subscheme 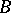(cf. Birational geometry).

For any linear system without fixed components 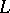on a smooth projective surface 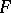there exists an integer 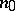such that if 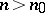, then the basic set of the complete linear system 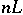is empty (Zariski's theorem). This is not true in the multi-dimensional case.

References

[1]	"Algebraic surfaces" Trudy Mat. Inst. Steklov. , 75 (1965) (In Russian) Zbl 0154.33002 Zbl 0154.21001
[2]	R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001