P-Sasakian manifold
A manifold similar to a Sasakian manifold. However, by its topological and geometric properties, such a manifold is closely related to a product manifold (unlike the Sasakian manifold, which is related to a complex manifold).
A Riemannian manifold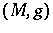 
endowed with an endomorphism 
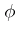of the tangent bundle 
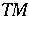, a vector field 
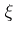and a 
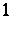-form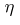 
which satisfy the conditions
 |
 |
 |
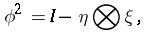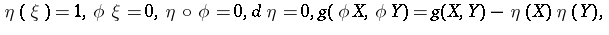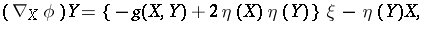for any vector fields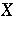 
, 
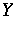tangent to 
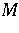, where 
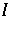and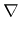 
denote the identity transformation on 
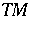and the Riemannian connection with respect to 
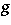, respectively, is called a P-Sasakian manifold [a3].
The structure group of the tangent bundle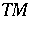 
is reducible to 
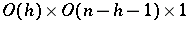, where 
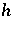is the multiplicity of the eigenvalue 
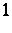of the characteristic equation of 
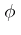and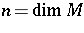 
.
Examples.
The hyperbolic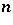 
-space form 
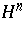. As a model, one can take the upper half-space 
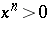in the sense of Poincaré's representation (cf. also Poincaré model). The metric of 
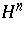is given by
 |
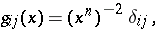where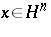 
, 
. The characteristic vector fiel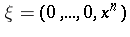d 
, and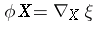 
for any vector field 
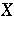tangent to 
.
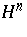The warped product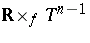 
of a real line 
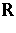and an 
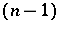-dimensional flat torus 
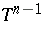, with 
.
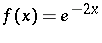Properties.
If a P-Sasakian manifold is a space form (cf. Space forms), then its sectional curvature is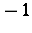 
[a2].
The characteristic vector field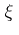 
of a P-Sasakian manifold is an exterior concurrent vector field [a2].
On a compact orientable P-Sasakian manifold, the characteristic vector field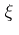 
is harmonic [a5].
A projectively flat P-Sasakian manifold is a hyperbolic space form of constant curvature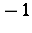 
[a5].
For the de Rham cohomology of a P-Sasakian manifold, the following result is known [a1]: Let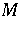 
be a compact P-Sasakian manifold such that the distribution annihilated by 
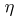is minimal. Then the first Betti number 
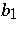does not vanish.
References
| [a1] | I. Mihai, R. Rosca, L. Verstraelen, "Some aspects of the differential geometry of vector fields" , PADGE , 2 , KU Leuven&KU Brussel (1996) |
| [a2] | R. Rosca, "On para Sasakian manifolds" Rend. Sem. Mat. Messina , 1 (1991) pp. 201–216 |
| [a3] | I. Sato, "On a structure similar to the almost contact structure I; II" Tensor N.S. , 30/31 (1976/77) pp. 219–224; 199–205 |
| [a4] | I. Sato, "On a Riemannian manifold admitting a certain vector field" Kodai Math. Sem. Rep. , 29 (1978) pp. 250–260 |
| [a5] | I. Sato, K. Matsumoto, "On P-Sasakian manifolds satisfying certain conditions" Tensor N.S. , 33 (1979) pp. 173–178 |
P-Sasakian manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=P-Sasakian_manifold&oldid=51320