Fedosov trace formula
From Encyclopedia of Mathematics
An asymptotic formula as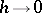 
for the "localized" trace of the exponential of a Hamiltonian 
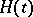. The leading terms of this expansion can be calculated in terms of the fixed points of the classical Hamiltonian flow associated to 
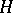(provided that it has only isolated fixed points, see below). Explicitly,
 |
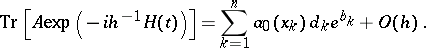Here, the meaning of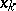 
, 
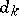and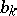 
is the following. First, 
is a pseudo-differential operator with compactly supported Weyl symbol (cf. also Symbol of an operator). Let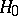 
and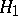 
be the homogeneous components of 
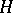, and denote by 
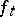the Hamiltonian flow associated to 
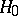(cf. also Hamiltonian system). The formula above is proved under the assumption that, on the support of 
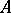, the flow 
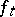has only isolated fixed points, denoted by 
. Then 
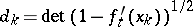and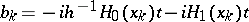 
. See [a1].
References
| [a1] | B. Fedosov, "Trace formula for Schrödinger operator" Russian J. Math. Phys. , 1 (1993) pp. 447–463 |
How to Cite This Entry:
Fedosov trace formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fedosov_trace_formula&oldid=50490
Fedosov trace formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fedosov_trace_formula&oldid=50490
This article was adapted from an original article by Victor Nistor (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article