Sperner theorem
Let  . A family
. A family  of subsets of
of subsets of 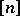 that are pairwise unrelated with respect to inclusion is called a Sperner family (or Sperner system) on
that are pairwise unrelated with respect to inclusion is called a Sperner family (or Sperner system) on  . Examples are the families
. Examples are the families
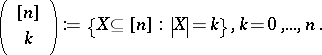 |
Since the binomial coefficients satisfy the inequalities
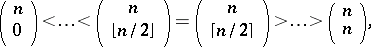 |
in these examples  , if
, if  is even, and
is even, and 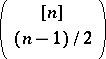 as well as
as well as 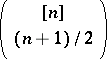 , if
, if  is odd, have maximum size. Sperner's theorem from 1928 states that these best examples have even maximum size among all Sperner families on
is odd, have maximum size. Sperner's theorem from 1928 states that these best examples have even maximum size among all Sperner families on 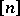 and that they are the only optimal families.
and that they are the only optimal families.
Given a Sperner family 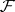 , let
, let 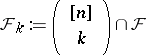 and
and 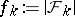 . In his original proof, E. Sperner used a shifting technique: Consider the smallest
. In his original proof, E. Sperner used a shifting technique: Consider the smallest 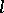 with
with 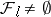 and replace
and replace 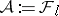 by its upper shadow
by its upper shadow
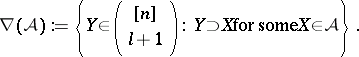 |
Double-counting easily yields 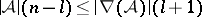 and, equivalently,
and, equivalently,
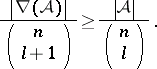 | (a1) |
Thus, each Sperner family can be shifted from below to the "middle" and, analogously, from above to the "middle" and thereby increasing its size.
The inequality (a1) holds for all 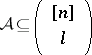 and all
and all  , and this property is called the normalized matching property of the lattice of subsets of
, and this property is called the normalized matching property of the lattice of subsets of 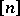 . If
. If 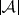 and
and  are fixed, the best possible estimate of the upper shadow, and, dually, of the lower shadow (replace
are fixed, the best possible estimate of the upper shadow, and, dually, of the lower shadow (replace 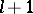 by
by 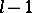 and superset by subset), is given by the Kruskal–Katona theorem.
and superset by subset), is given by the Kruskal–Katona theorem.
Sperner's theorem follows also easily from the inequality
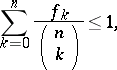 |
which can be obtained by counting in two different ways the number of pairs 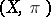 where
where  ,
, 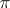 is a permutation of
is a permutation of 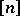 and
and 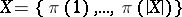 . This inequality was proved independently by D. Lubell, S. Yamamoto and L. Meshalkin, and is hence called the LYM inequality; a more general form of it was given by B. Bollobás.
. This inequality was proved independently by D. Lubell, S. Yamamoto and L. Meshalkin, and is hence called the LYM inequality; a more general form of it was given by B. Bollobás.
An essential part of Sperner theory consists of the study of other partially ordered sets having analogous properties, e.g. LYM posets and Peck posets (cf. Sperner property).
Details can be found in [a1].
References
| [a1] | K. Engel, "Sperner theory" , Cambridge Univ. Press (1997) |
| [a2] | E. Sperner, "Ein Satz über Untermengen einer endlichen Menge" Math. Z. , 27 (1928) pp. 544–548 |
Sperner theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sperner_theorem&oldid=50377