Isotropic submanifold
From Encyclopedia of Mathematics
A term used in symplectic and contact geometry. In the case of a symplectic manifold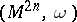 
, where 
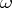is a closed, non-degenerate 
-form, it denotes a submanifold 
of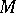 
such that 
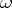restricts to zero on the tangent bundle of 
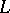. In the case of a contact manifold 
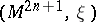, where locally 
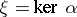with a 
-form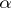 
satisfying 
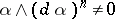, it refers to a submanifold which is everywhere tangent to 
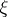. In either case an isotropic submanifold is of dimension at most 
. An isotropic submanifold of maximal dimension 
is called a Lagrange submanifold in the former case, and a Legendre submanifold in the latter.
References
| [a1] | V.I. Arnold, A.B. Givental, "Symplectic geometry" V.I. Arnold (ed.) S.P. Novikov (ed.) , Dynamical Systems IV , Encycl. Math. Sci. , 4 , Springer (1990) |
How to Cite This Entry:
Isotropic submanifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isotropic_submanifold&oldid=50362
Isotropic submanifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Isotropic_submanifold&oldid=50362
This article was adapted from an original article by H. Geiges (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article