Buser isoperimetric inequality
From Encyclopedia of Mathematics
For a compact Riemannian manifold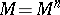 
, let 
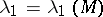be the smallest positive eigenvalue of the Laplace–Beltrami operator (cf. also Laplace–Beltrami equation) of 
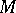and define the isoperimetric constant of 
by
 |
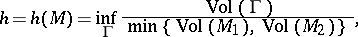where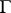 
varies over the compact hypersurfaces of 
which partition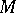 
into two disjoint submanifolds 
, 
.
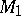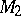If the Ricci curvature of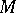 
is bounded from below,
 |
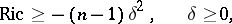then the first eigenvalue has the upper bound
 |
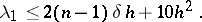Note that a lower bound for the first eigenvalue, without any curvature assumptions, is given by the Cheeger inequality
 |
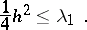References
| [a1] | P. Buser, "Über den ersten Eigenwert des Laplace–Operators auf kompakten Flächen" Comment. Math. Helvetici , 54 (1979) pp. 477–493 |
| [a2] | P. Buser, "A note on the isoperimetric constant" Ann. Sci. Ecole Norm. Sup. , 15 (1982) pp. 213–230 |
| [a3] | I. Chavel, "Riemannian geometry: A modern introduction" , Cambridge Univ. Press (1995) |
How to Cite This Entry:
Buser isoperimetric inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Buser_isoperimetric_inequality&oldid=50321
Buser isoperimetric inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Buser_isoperimetric_inequality&oldid=50321
This article was adapted from an original article by H. Kaul (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article