Olevskii transform
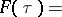 | (a1) |
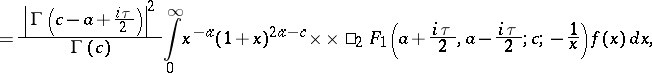 |
where  is a Gauss hypergeometric function. It was introduced by M.N. Olevskii in [a1].
is a Gauss hypergeometric function. It was introduced by M.N. Olevskii in [a1].
Letting  , one obtains the Mehler–Fock transform. By changing the variable
, one obtains the Mehler–Fock transform. By changing the variable  and the respective parameters of the Gauss function, one obtains the Fourier–Jacobi transform [a2].
and the respective parameters of the Gauss function, one obtains the Fourier–Jacobi transform [a2].
One can show that the Olevskii transform is the composition of the Kontorovich–Lebedev transform and the Hankel transform (cf. Integral transform; Hardy transform).
The Gauss function in the integral (a1) is the hypergeometric series for  and for
and for  one can understand it as an analytic continuation, which can be obtained from the Mellin–Barnes integral representation [a3].
one can understand it as an analytic continuation, which can be obtained from the Mellin–Barnes integral representation [a3].
The following integral transform is also called the Olevskii transform. It is an integral over the index  of the Gauss function,
of the Gauss function,
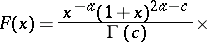 | (a2) |
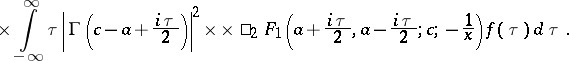 |
Here,  is an arbitrary odd function belonging to the space
is an arbitrary odd function belonging to the space 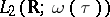 , where
, where
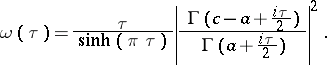 |
The transform (a2) maps this space onto the space  and the Parseval equality holds:
and the Parseval equality holds:
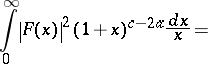 |
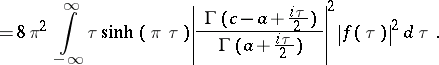 |
References
| [a1] | M.N. Olevskii, "On the representation of an arbitrary function by integral with the kernel involving the hypergeometric function" Dokl. Akad. Nauk SSSR , 69 : 1 (1949) pp. 11–14 (In Russian) |
| [a2] | T.H. Koornwinder, "Jacobi functions and analysis on noncompact semisimple Lie groups" , Special Functions: Group Theoretical Aspects and Applications , Reidel (1984) pp. 1–85 |
| [a3] | S.B. Yakubovich, "Index transforms" , World Sci. (1996) pp. Chap. 7 |
Olevskii transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Olevskii_transform&oldid=50300