Hyperbolic cross

A summation domain of multiple Fourier series (cf. also Partial Fourier sum). Let be an integrable periodic function of variables defined on , . It has an expansion as a Fourier series, , , , . Unlike in the one-dimensional case, there is no natural ordering of the Fourier coefficients, so the choice of the order of summation is of great importance.

Let with all coordinates positive, . Consider the differential operator with periodic boundary conditions on . Then the eigenvalues (cf. Eigen value) of are , while the corresponding eigenfunctions are 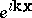. The partial sums of the Fourier series corresponding to the eigenfunctions with all eigenvalues 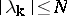are called hyperbolic partial Fourier sums of order 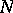(or hyperbolic crosses). This approach, in which the method of summation of the Fourier series is defined by the differential operator, is due to K. Babenko [a1], who applied it to various problems in approximation theory (e.g., Kolmogorov widths, -entropy, etc.). Subsequently the hyperbolic cross itself became the object of study in connection with Lebesgue constants, the Bernshtein inequality, etc. Also, this approach initiated a detailed study and applications of spaces of functions with bounded mixed derivative (in ).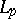

Many of these and related classes, as well as various problems in approximation theory, are considered in [a2]. This method of summation has also been applied to other series expansions, e.g., multiple wavelets systems.

References

[a1]	K. Babenko, "Approximation of periodic functions of many variables by trigonometric polynomials" Soviet Math. , 1 (1960) pp. 513–516 Dokl. Akad. Nauk. SSSR , 132 (1960) pp. 247–250
[a2]	V. Temlyakov, "Approximation of periodic functions" , Nova Sci. (1993)